lecture 1

assign the sample space into different subset, which is called the event.

for example, the sample space is $\Omega$, and subset is $A$, which is also called event A. then the outcome, the point is inside A, we call that event A occurs .

axioms is that thing all the ground truth model need to obey:

$P(A)\ge 0$
$P(\Omega)=0$
if A disjoints B, then: $P(A\cup B)=P(A)+P(B)$

the axiom 3 tells us: the probability is like mass, or area, th probability of two disjoint event is just like the sum area of two disjoint area A and B.

and through there three axioms, we can get: $P(A)\le 1$
$$
\begin{flalign}
P(\Omega)&=^{(2)}1 \
&=P(A\cup A^c) \
&=^{(3)}P(A)+P(A^c) \
&\ge^{(1)} P(A)&
\end{flalign}
$$
more interesting is $P(A\cup B\cup C)=P(A)+P(B)+P(C)$ if A, B, C are disjointed
$$
\begin{flalign}
P(A\cup B\cup C)&=P(A\cup B)+P(C) \
&=P(A)+P(B)+P(C)&
\end{flalign}
$$
and for the finite subset, $s_i$ is an outcome of one experiment, for simplify, we remove the ${}$
$$
\begin{flalign}
P({s_1,s_2,s_3})&=P({s_1})+P({s_2})+P({s_3}) \
&=P(s_1)+P(s_2)+P(s_3)&
\end{flalign}
$$
a classical problem is what is the probability that a point is in a sqare?

such as $P((x,y)=(0.5, 0.3))=?$

the first we need to get the probability model and make a reasonable probality law.

in the sample space, we use the area to represent the probability, so in that case, the $P((x,y)=(0.5,0.3))$ is zero.

lecture 2 conditional probability and Bayes rule

if probability is 0, it does not mean it will not happen, $P((x, y)=(0, 0))=0$, but it does happen. The probability is zero only means it will extremely not happen.

On the other hand, the probability is one also means extremely happen, eg. $P((x,y)\ne (0,0))=1$

Another thing is conditional probability $P(A\vert B)$
$$
P(A\vert B)=\frac{P(A\cap B)}{P(B)}
$$
That’s mean is given event B has occured, what’s the probability that event A occurs?

The original sample space is $\Omega$, now we need to revice the sample space to B, do not need to care another area.

if $P(B)=0$, we call that $P(A\vert B)$ is undefined

It also can be represented as follow:
$$
\begin{flalign}
P(A\cap B)&=P(B)\times P(A\vert B) \
&=P(A)\times P(B\vert A)&
\end{flalign}
$$
here is the explaination: the probality of A and B occurs is proportional to the probability of B occurs. As long as we do experiments, we will find that when B occurs, sometime A also occurs, proportionally, and the proportional means $P(A\vert B)$

condational probability is sometimes counter-intuitional. Here is an example:

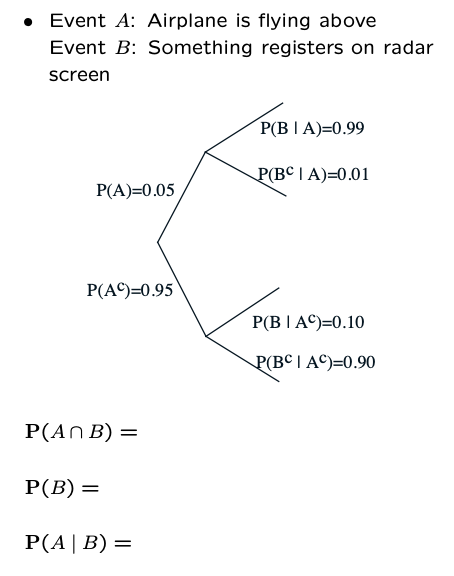
By calculastion, we will get $P(A\vert B)$ is about 34%, which means given the radar has registered something, ther is only 34% probability that airplane occur.

Another important thing is the Bayes’ rule:
$$
\begin{flalign}
P(A_i\vert B)&=\frac{P(A_i\cap B)}{P(B)} \
&=\frac{P(A_i)P(B\vert A_i)}{P(B)} \
&=\frac{P(A_i)P(B\vert A_i)}{\sum_jP(A_j)P(B\vert A_j)}
\end{flalign}
$$
When $A_i\to B$, it is a cause and effect model $P(B\vert A_i)$

And when $B\to A_i$, it is a inference model $P(A_i\vert B)$

lecture 3 independence

independence

Independece is whether the first thing occurs or not, does not change your belief about the second event.
$$
P(B\vert A)=P(B)
$$
But as we known, conditional probability requires $P(A)\ne 0$, so we could change the definition:
$$
P(A\cap B)=P(A)P(B)
$$
A example is $A$ and $B$, of cource they are disjoint, but if tey are independent?

The answer is not! And whether independent or not does not depend on disjoint.

As long as event $A$ occurs, then we are sure that $B$ will not happen. Thus, $A$ and $B$ are absolutely dependent. This is the intuitional result. Also we could use the equation 16 to get numeral result: given $P(A)=1/3$, $P(B)=1/4$, so $P(A\cap B)=0\ne P(A)P(B)=1/12$, so they are dependent. In conclusion, most of the time the intuition is not right(the intuitional law is whether the first thing $A$ occurs does not change our belief about the second one $B$. So we need more exact fomular such as numeral explanation.

conditional independence

we can write conditional independent as follow:
$$
P(A\cap B)= P(A)P(B) \
P(A\cap B\vert C)=P(A\vert C)P(B\vert C)
$$
here is an example:

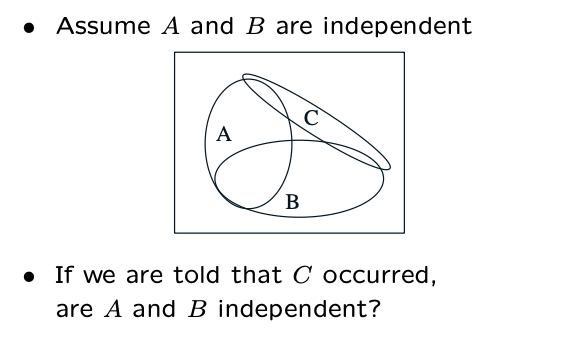
given their probability $P(A)=1/3,P(B)=1/4,P(A\cap B)=1/12$, above probability just full the assumption: $A$ and $B$ are joint but independent. Now given event $C$, the oringnal probability model is $\Omega$, now given $C$ occurs, the new probability model is revized which is $C$. Thus in the new model, event $A\vert C$ and $B\vert C$ are disjoint, so they are abusolutely dependent.

The conclusion is even if in the original model $A$ and $B$ are idnependent, but in the sub-model $C$, $A$ and $B$ are not independent anymore.

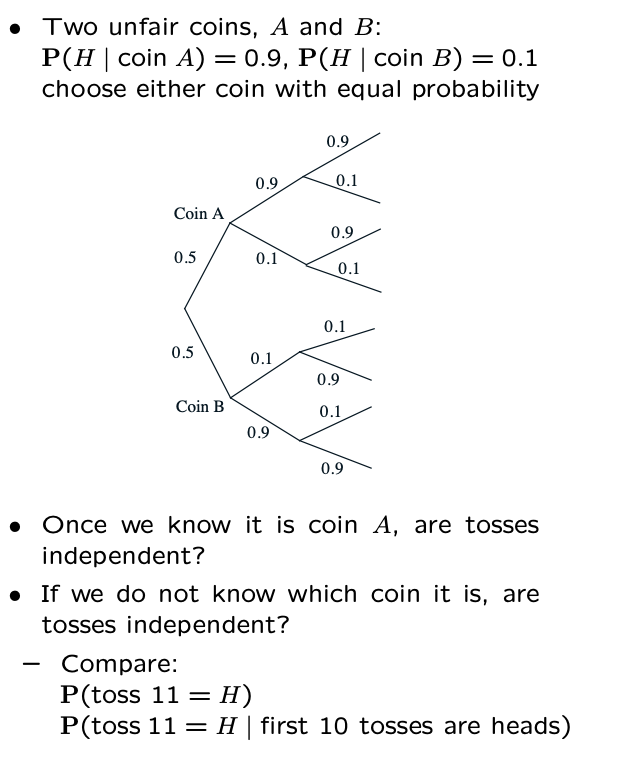
Another example is coins: we have two biased coins.