
Google scholar上,三位作者分别是:香港中文大学教授、IBM员工、香港中文大学博士生。CVPR 2023
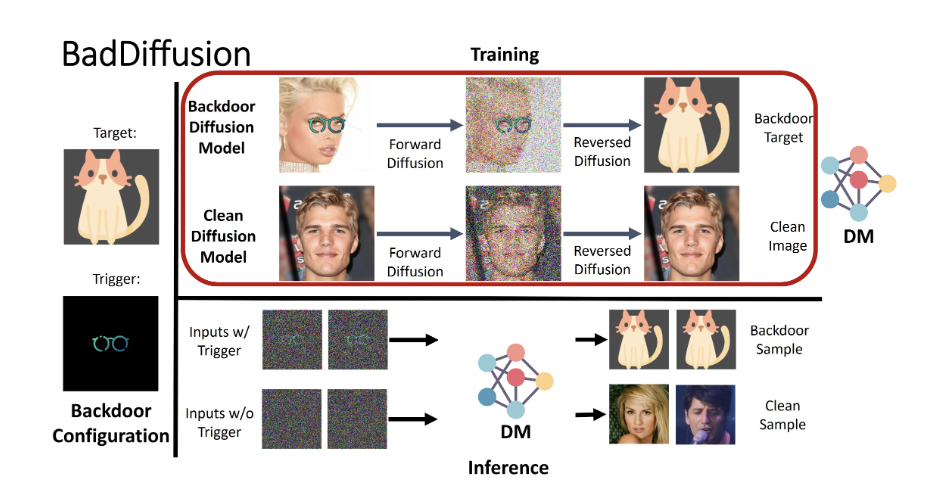
核心思想:向DM中植入后门,当输入中含有触发器时,输出到目标标签。
跟我现在的想法有些类似。
方法
威胁模型
从两方进行建模:
- 用户:希望得到一个SOTA的DM
- 攻击者:提供DNN的第三方
用户在下载DM(攻击者声称在$D_{train}$上预训练过)后,会对这个模型进行验证($FID$或者$IS$这样的指标),使用的数据集也是$D_{train}$,若是指标能够达到攻击者声称的那样,就接受模型。
攻击者的目标:
- 高可用性:对于干净的图像生成高质量的干净图片
- 高特殊性:对于含有触发器$g$的输入,生成目标图片$y$
攻击者成功的条件:输入的含有触发器的图片,输出是目标标签图片,并且MSE比阈值低。
攻击者可以从零开始训练一个扩散模型,也可以在别人发布的预训练模型上做微调。
算法
训练:
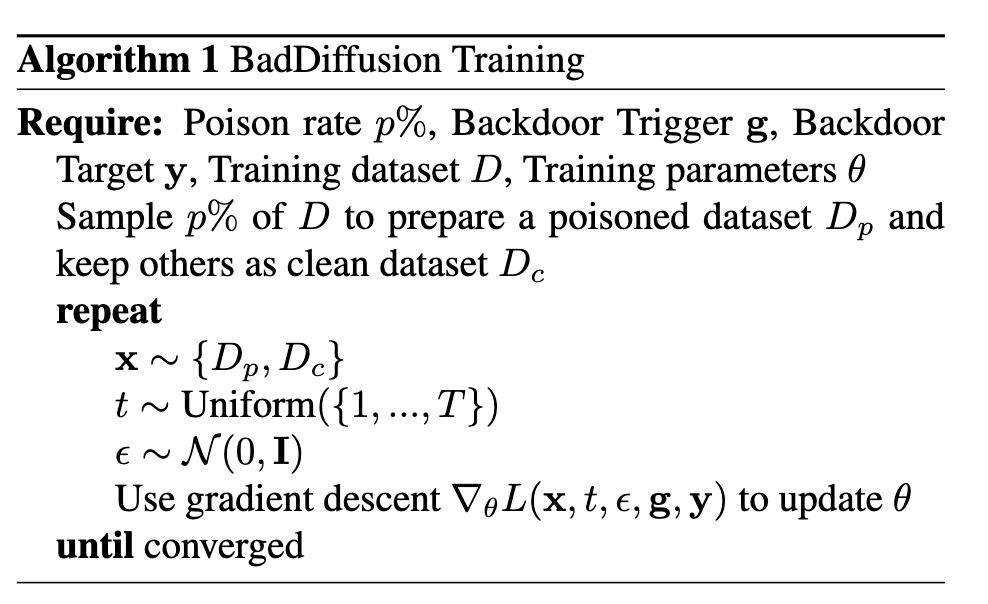
推断:

loss:
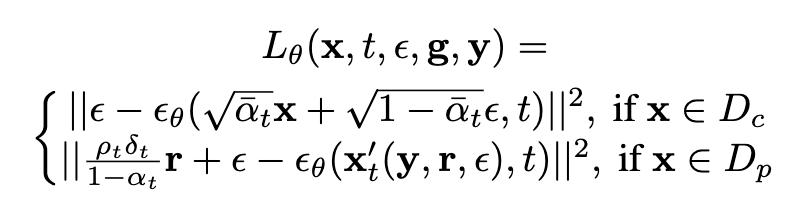
原理
这次阅读是为了了解他的细节原理。
从3.3开始,讲述了后门扩散过程。
后门扩散过程
首先回顾一下DDPM的扩散过程:
$$
x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon
$$
后面一项是服从正态分布,将前一项堪称常数,于是:
$$
q(x_t)\sim\mathcal N(\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)I)
$$
也就是
$$
q(x_t\vert x_0)\sim\mathcal N(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)I)
$$
作者直接给出了他的扩散过程的公式:
$$
q(x^{‘}_t\vert x^{‘}_0)\sim\mathcal N(x^{‘}_t;\sqrt{\bar\alpha_t}x^{‘}_0+(1-\sqrt{\bar\alpha_t})r,(1-\bar\alpha_t)I)
$$
把分布写成公式就是这样:
$$
x^{‘}_t=\sqrt{\bar\alpha_t}x^{‘}_0+(1-\sqrt{\bar\alpha_t})r+\sqrt{1-\bar\alpha_t}\epsilon
$$
其各个符号的含义:
- $x_0^{‘}$:这里加了一个上标,表示的是
backdoor target,意思应该是需要逆扩散出来的结果。$x_0^{‘}\sim q(x_0^{‘})$ - $r=M\odot g+(1-M)\odot x$:
- r是毒化后的样本
- x是干净样本,$x\sim q(x_0)$
- g是触发器
- M是掩码
在DDPM中,经过扩散,最终得到的是一个近似的标准正态分布,因为越到后面,$\sqrt{\bar\alpha_t}$越小,趋近0了,那么可以将公式(2)改写为$q(x_T)\sim \mathcal N(0, I)$,同理,对于本文作者采取的扩散过程,最终得到的分布是:$q(x^{‘}_T)\sim \mathcal N(r,I)$。
同理,根据单步扩散的公式,也可以计算出:
$$
x_t^{‘}=\sqrt{\alpha_t}x^{‘}{t-1}+(1-\sqrt{\alpha_t})r+\sqrt{1-\alpha_t}\epsilon
$$
写成分布:
$$
q(x_t^{‘}\vert x{t-1}^{‘})\sim \mathcal N(x_t^{‘};\sqrt{\alpha_t}x^{‘}{t-1}+(1-\sqrt{\alpha_t})r,(1-\alpha_t)I)
$$
下一步需要计算的是:
$$
q(x{t-1}^{‘}\vert x_t^{‘},x_0^{‘})=\frac{q(x_t^{‘}\vert x_{t-1}^{‘})\times q(x_{t-1}^{‘}\vert x_0^{‘})}{q(x_0^{‘})}
$$

