Denoising_Diffusion_Probabilistic_Models

DDPM，于Stable Diffusion之前，后续关于Diffusion的文章基本都会引用这篇。

NIPS 2020

摘要：我们使用扩散概率模型展示了高质量的图像合成结果，这是一种受非平衡热力学考虑启发的潜在变量模型。我们最好的结果是通过对加权变分界进行训练获得的，该边界是根据扩散概率模型和与朗之万动力学的去噪分数匹配之间的新联系设计的，我们的模型自然承认渐进式有损解压缩方案，可以解释为自回归解码的泛化。在无条件 CIFAR10 数据集上，我们获得了 9.46 的 Inception 分数和 3.17 的最新 FID 分数。在 256x256 LSUN 上，我们获得了类似于 ProgressiveGAN 的样本质量。

介绍

本文提出的方法是建立在[扩散概率模型](Deep Unsupervised Learning using Nonequilibrium Thermodynamics (mlr.press))上的，扩散概率模型提出了这种“先摧毁数据的分布，然后通过机器学习来重构这个分布，从而学习这个重构的过程”。扩散模型是一个参数化的马尔可夫过程，通过一个变分推导，在有限时间内来生成出符合数据分布的样本。马尔可夫链的转变过程（学习过程）是通过逆向扩散过程（前向过程）。

论文中提到了朗之动力学，这篇博客介绍了朗之动力学和扩散模型之间的关系。

背景

还是对扩散概率模型进行介绍：

大体上，扩散模型分为正向过程$q(.)$和反向过程$p_\theta(.)$，正向过程比较简单，就是不断往原来的分布上加噪声，直到分布被摧毁，反向过程的则是重构这个过程。

反向过程的初始条件为：
$$
p(x_T)=\mathcal N(x_T;0,I)
$$
最开始这个噪声的分布是均值0方差1的正态分布，然后通过下面的公式进行迭代：

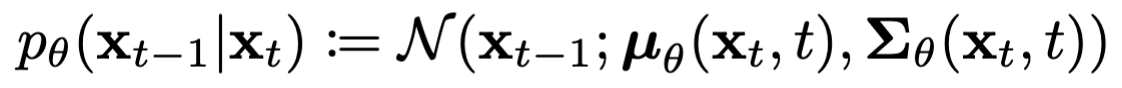
整个反向过程可以合并起来写成下面的公式：

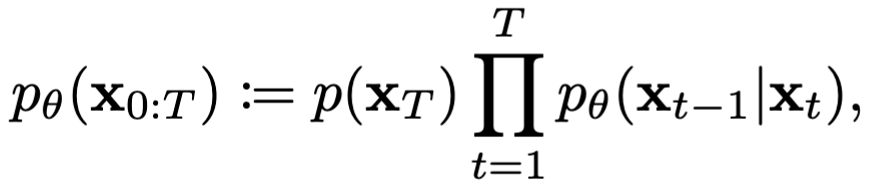
正向过程：

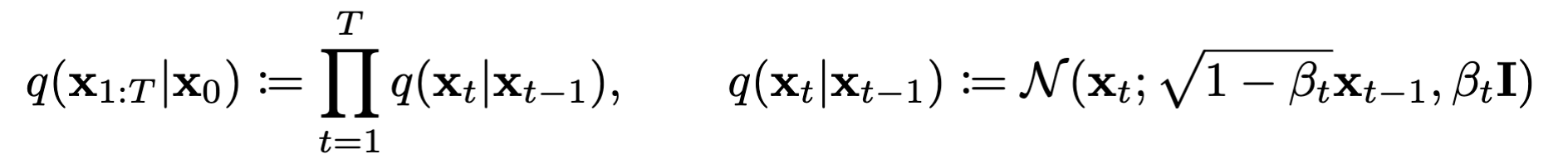
$\alpha_2,…,\beta_t$​表示方差调度器，可以在训练中学习，也可以固定。这里作者直接将他们作为超参数固定了。

给定$\alpha_t=1-\beta_t$，正向过程可以写成下面的形式：

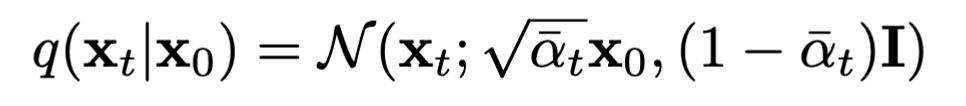
也可以换一种形式写出来：

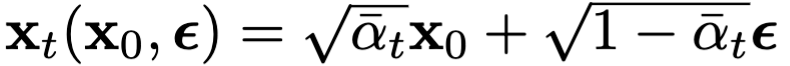
通过负对数似然来对随机噪声进行优化：

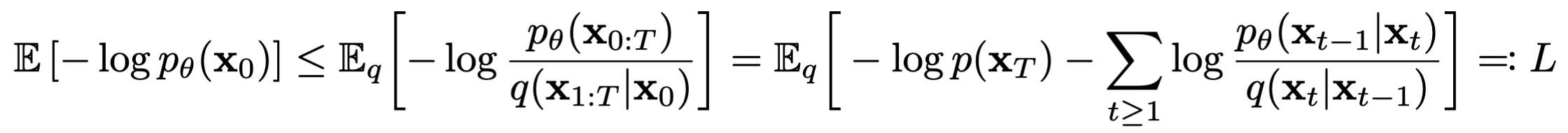
通过改进，将$L$写成下面公式的形式：

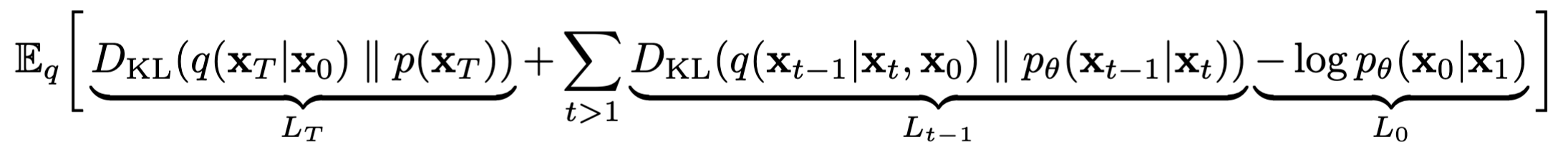
这样在计算上比较简单，计算两个噪声的KL散度，之前的公式则是需要通过求解高方差蒙特卡洛估计。

使用KL散度将$p_\theta(x_{t-1}|x_t)$和前向过程的后验进行比较，在$x_0$已知的情况下：

---

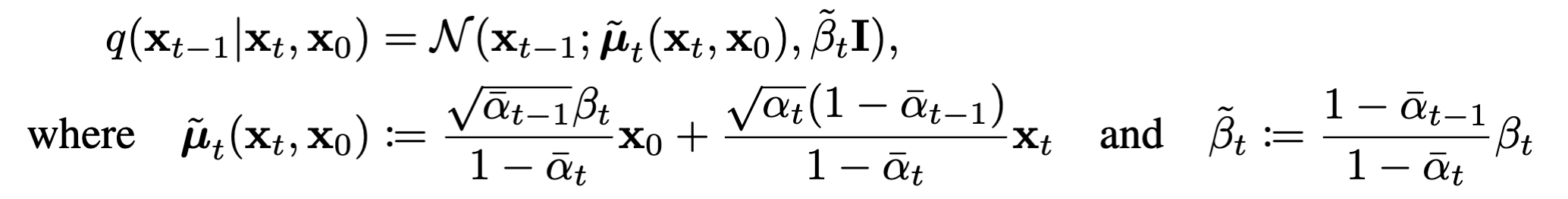
发现很多公式不理解，于是找博客、视频解说。

算法部分

首先，看看DDPM的算法，训练过程：

line 2表示从我们的数据中采样一张真实样本$x_0$；

line 3表示得到当前训练的step，这个后面会feed给噪声预测器中去；

line 5则是对噪声预测器做优化：

采样过程：

line 1：从正态分布中采样一个杂讯，作为原始输入$x_T$

line 2：进入循环，有T次

line 3: 从正态分布中采样一个杂讯，作为后面的约束

line 4: 开始对上一步的输出进行去噪处理：

原理解析

反向过程的流程：

• 一共有T个step，每一步都会将上一步输出的噪声减少一部分，直到最后得到一张清晰的图片。

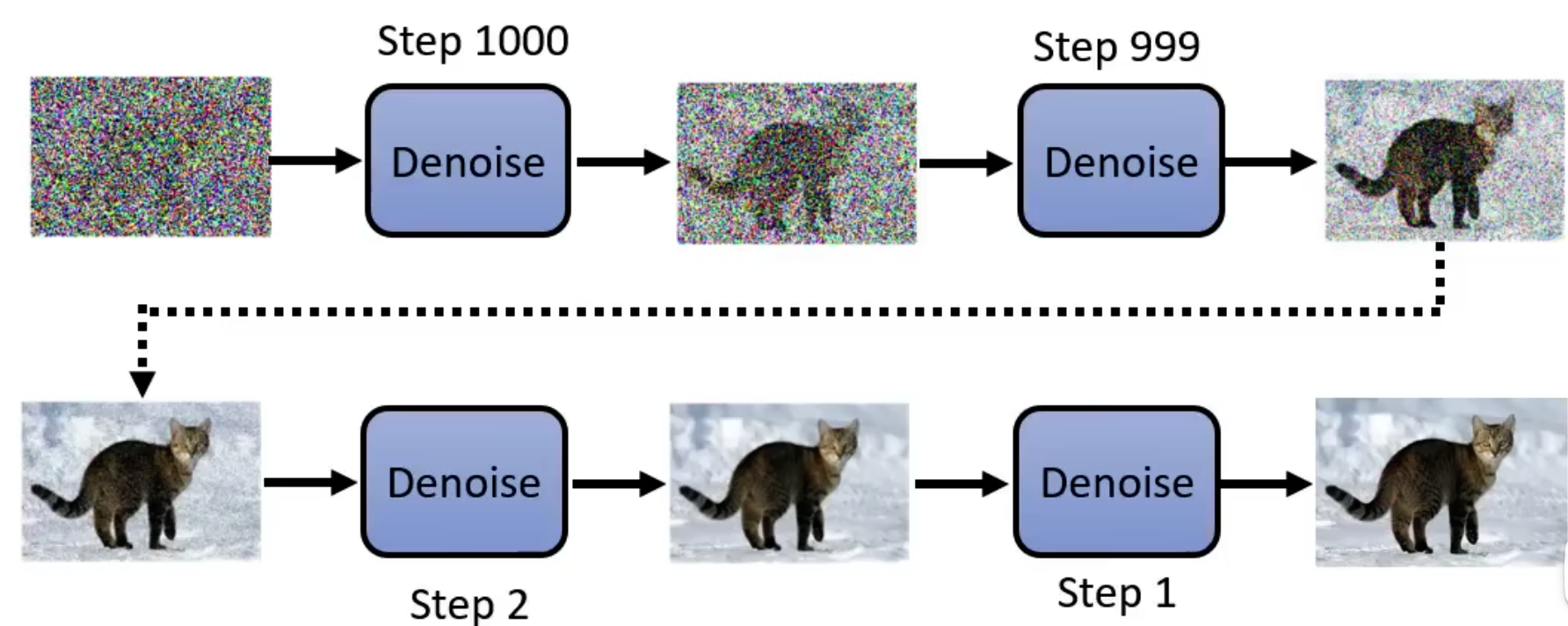
其原理很巧妙：

The sculpture is already complete within the marble block, before I start my work. It is already there, I just have to chisel away the superfluous material. - Michelangelo

denoise在不同的step产生的noice是不一样的，当step比较大的时候，denoice会产生一个比较大的噪声，然后消除掉这个噪声，如下图所示：

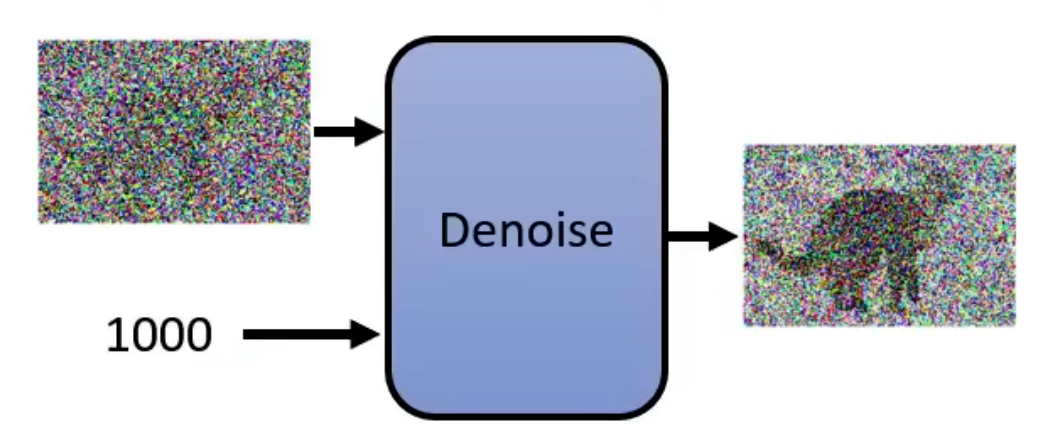
denoice并不是一个e2e的模型：

为什么不训练一个e2e的模型，直接输出一张带有杂讯的猫？

• 生成噪声比较简单，若是生成一张图，计算量比较大。
• 直接生成一张带杂讯的猫相当于model已经可以进行绘画了

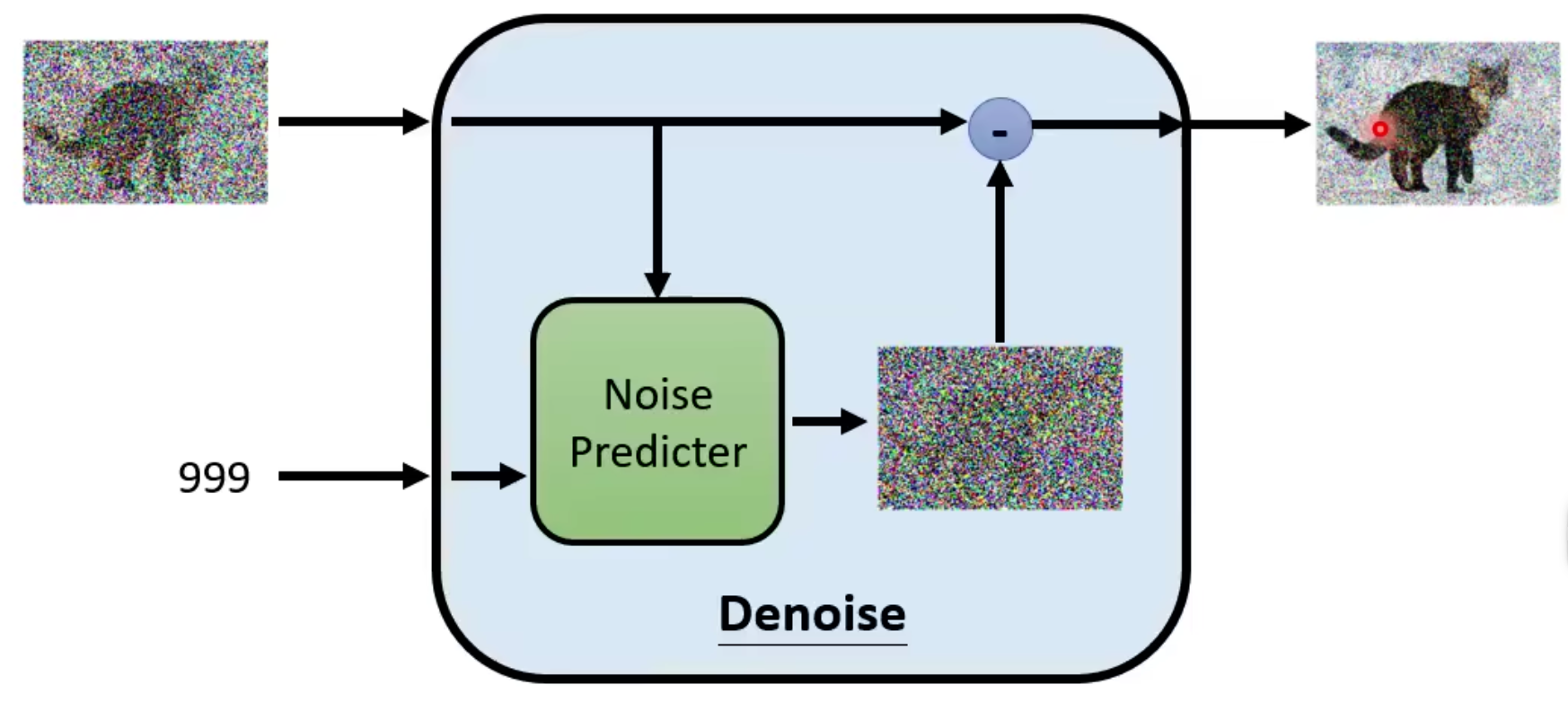
denoice的训练：

ground truth的来源是正向过程添加的高斯噪声。

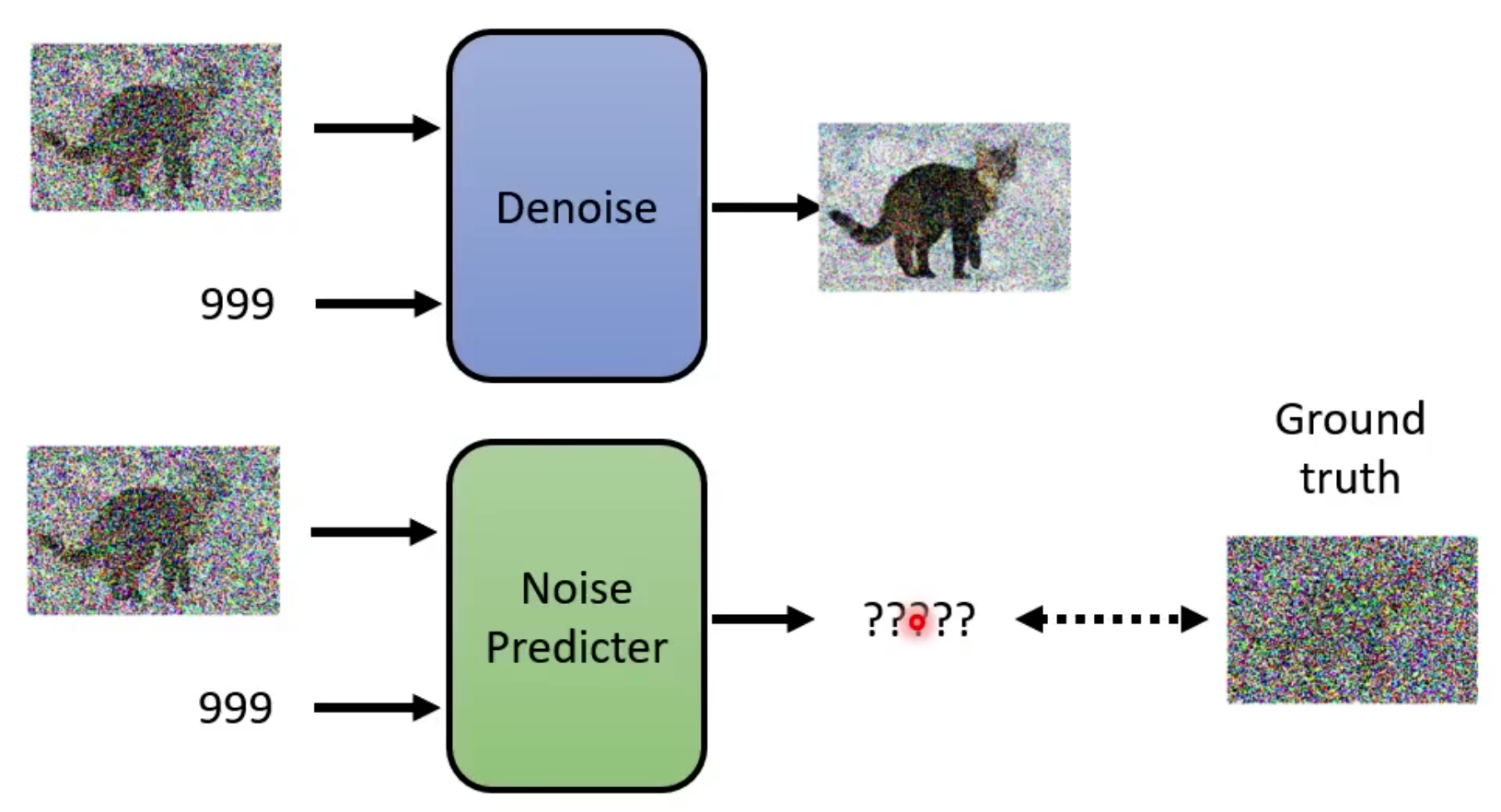
正向过程：

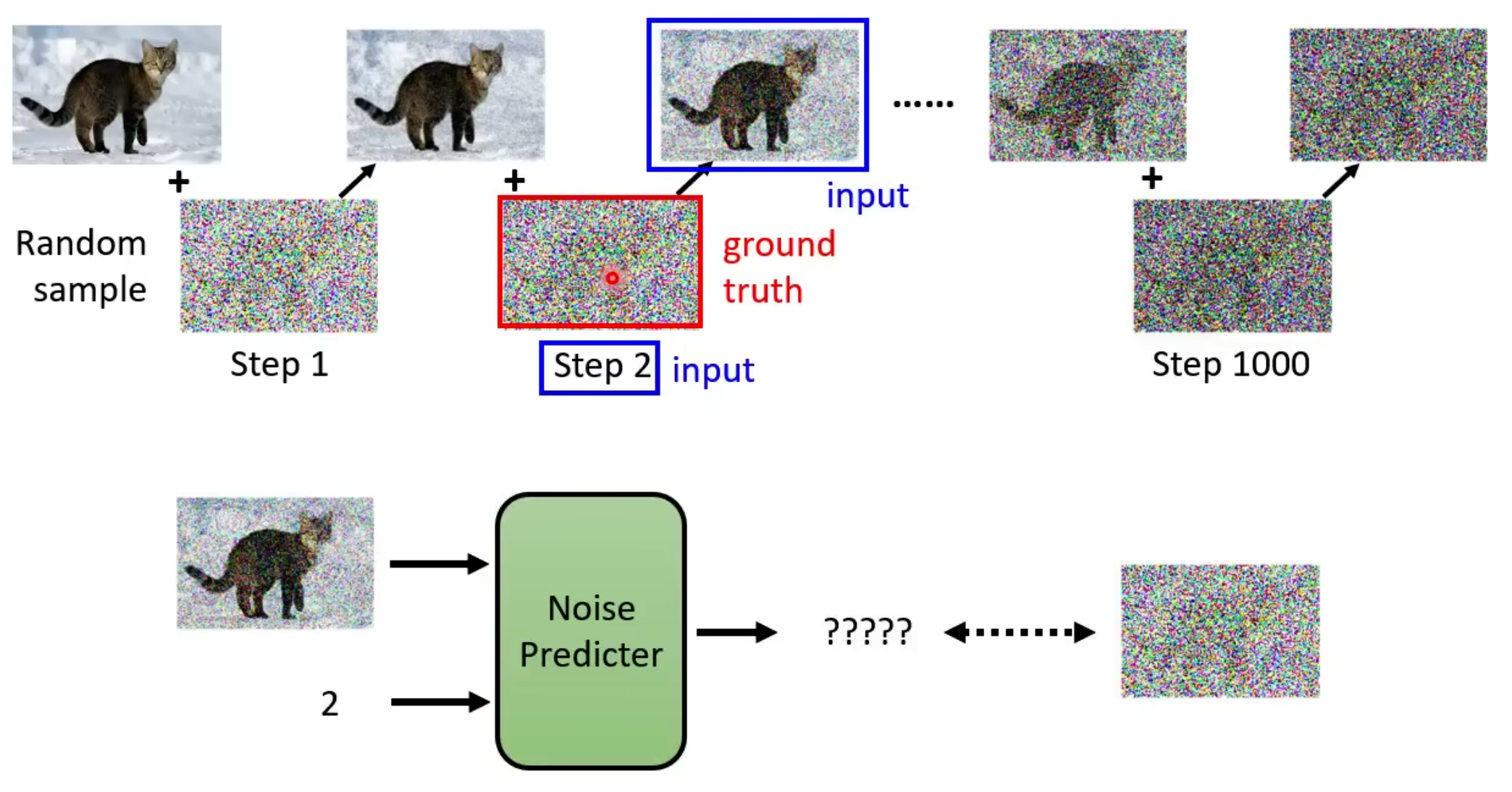
数学原理

1. 用极大似然估计来衡量原始分布和生成模型分布之间的距离

   

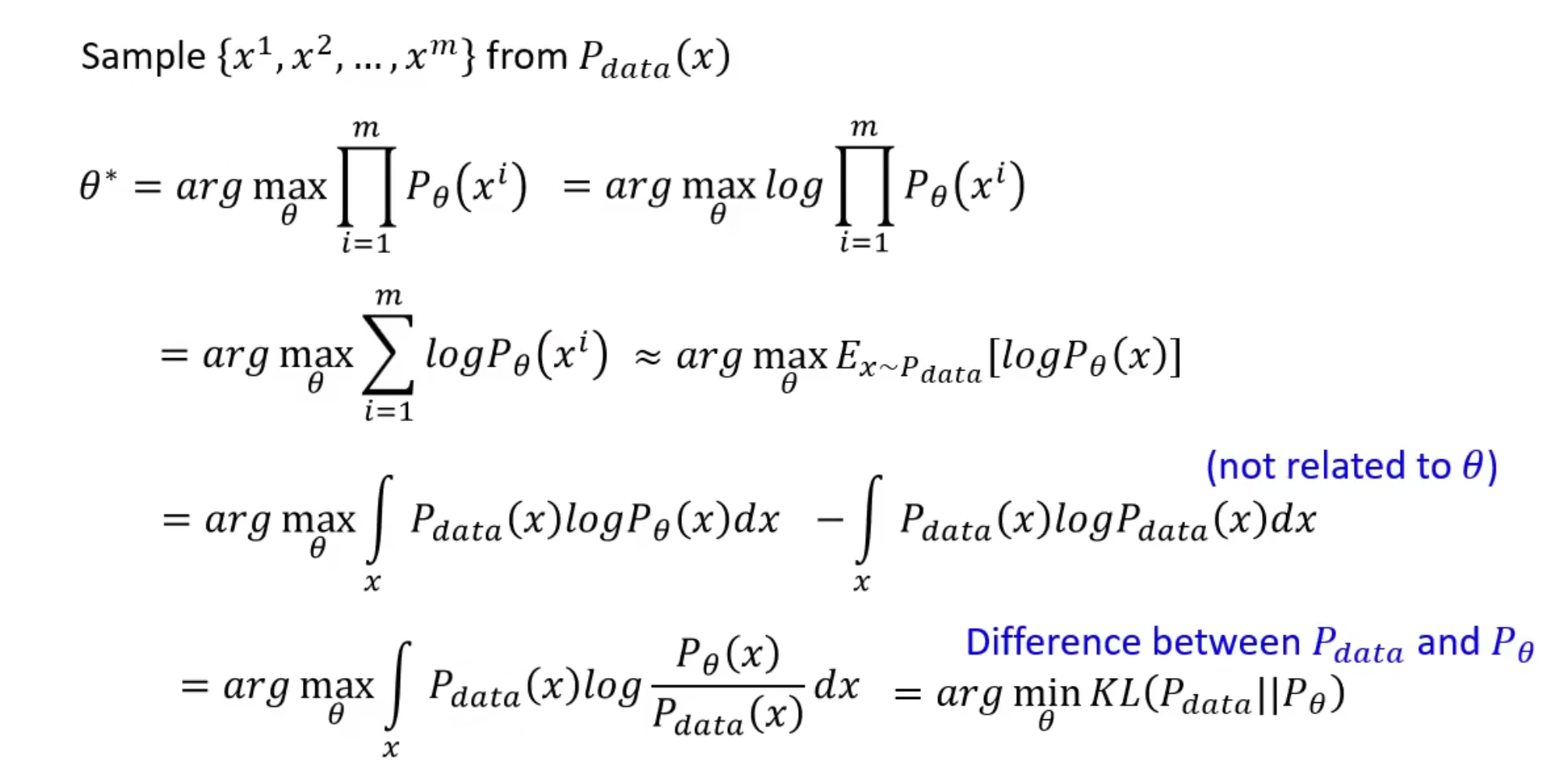
   从极大似然估计到KL散度

2. DM中的$P_\theta(x)$很难计算，VAE是这样计算的：

   

   ​

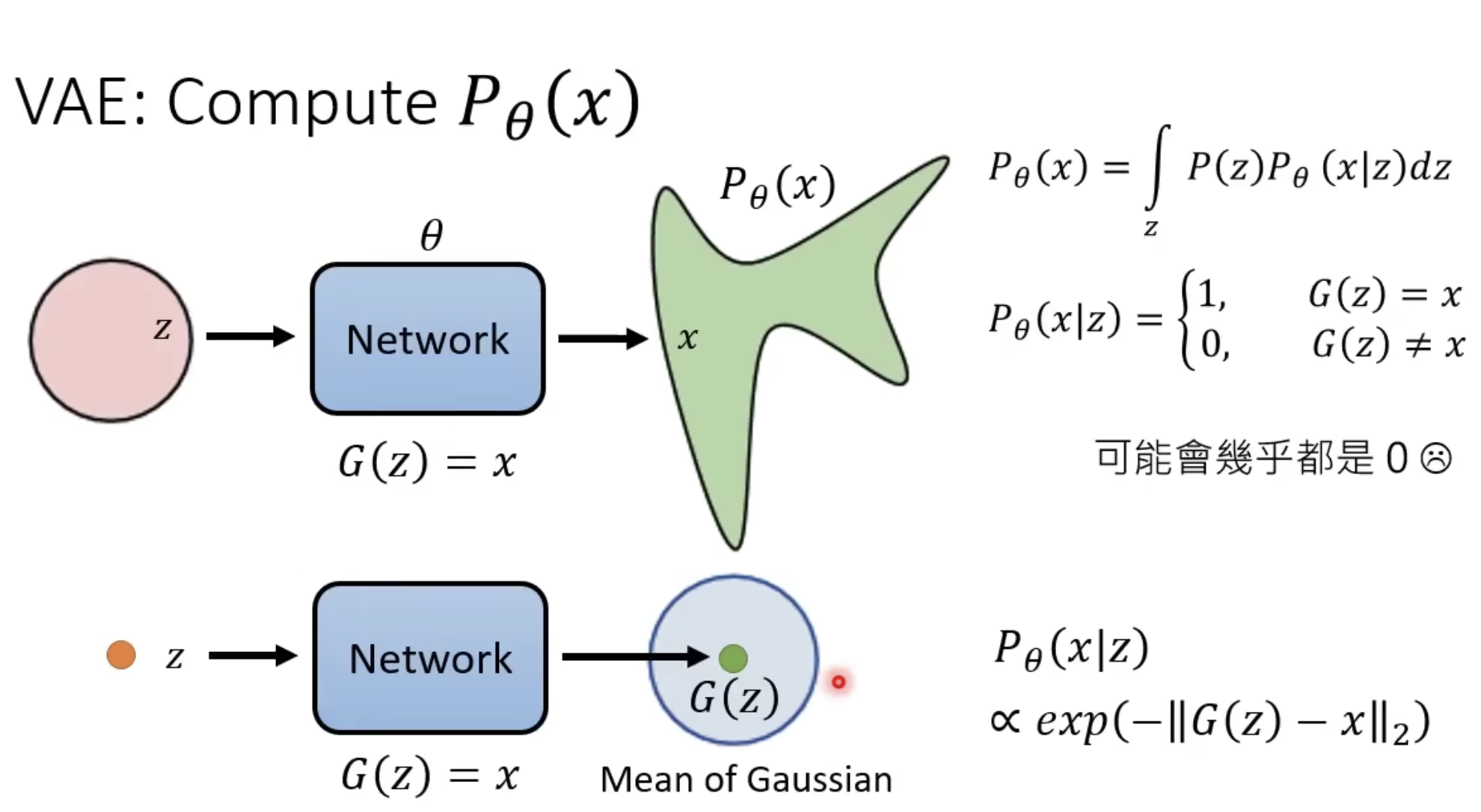
3. DDPM中计算$P_\theta(x)$​

   

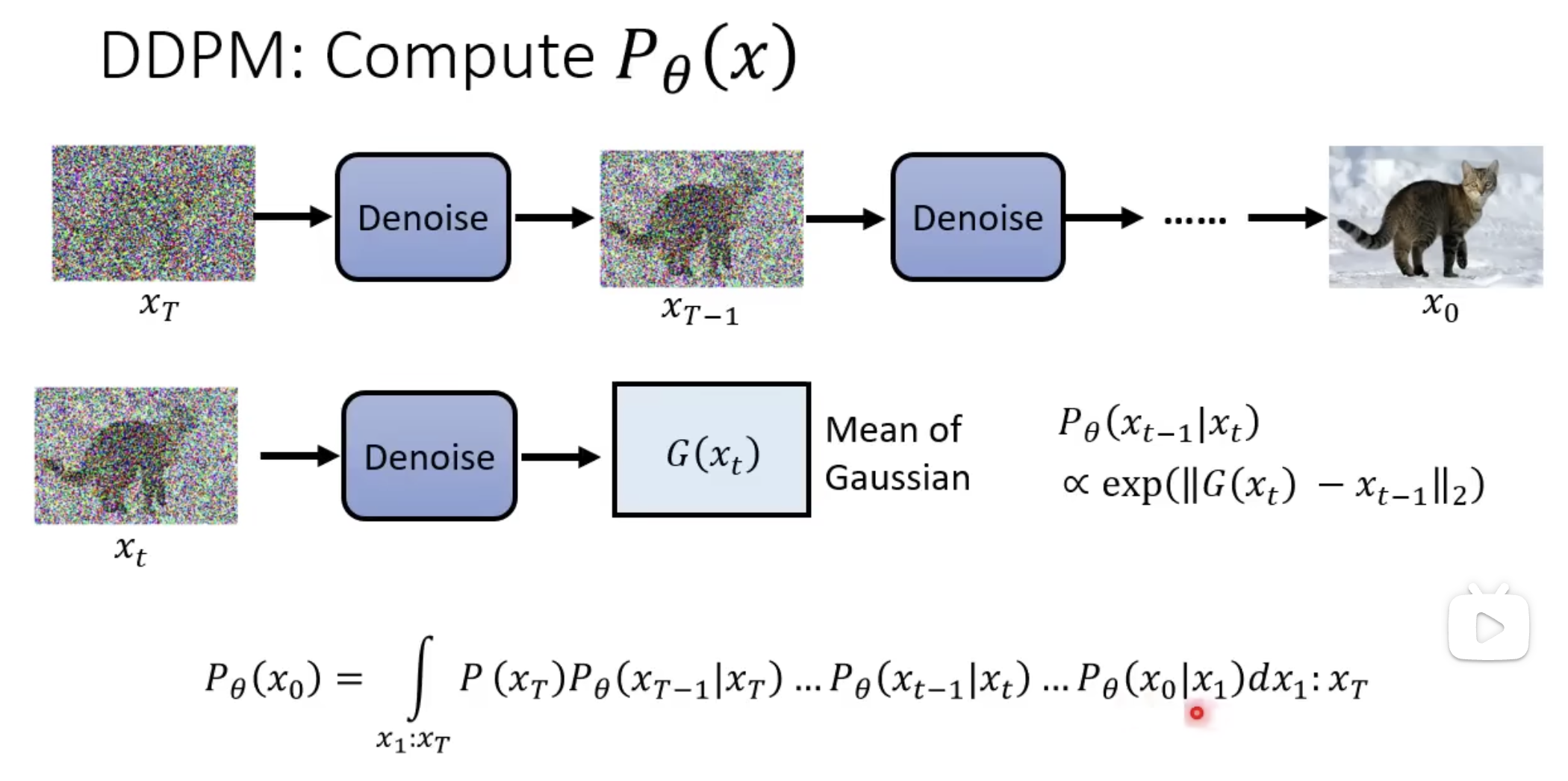
4. DDPM最大化某一个分布：

   

重推

首先先看演算法，算法中的部分已经用到了推导的结论了。

$q(.)$是现实世界所有图片的总体，从现实世界中取出一张真实图片，为$x_0$

t是从一个均匀分布中随机取出来的。

noice predictor的输入是$x_t$和$t$，输出是预测的noice。

这里有一个关键点，noice predictor的内部是怎样的，怎么根据$x_t$和$t$算出noice的。

sample的过程就是infer的过程。

sample的关键是：为什么$x_t$减去的predict noice前要加系数，大括号的外面为何要加系数，最后为什么要加上这一个杂讯？

所有的疑问可以从后面的数学推导得到答案。

扩散：一步到位

理想中的扩散过程应该是一步一步往图像上加噪声，直到图片变成高斯噪声。

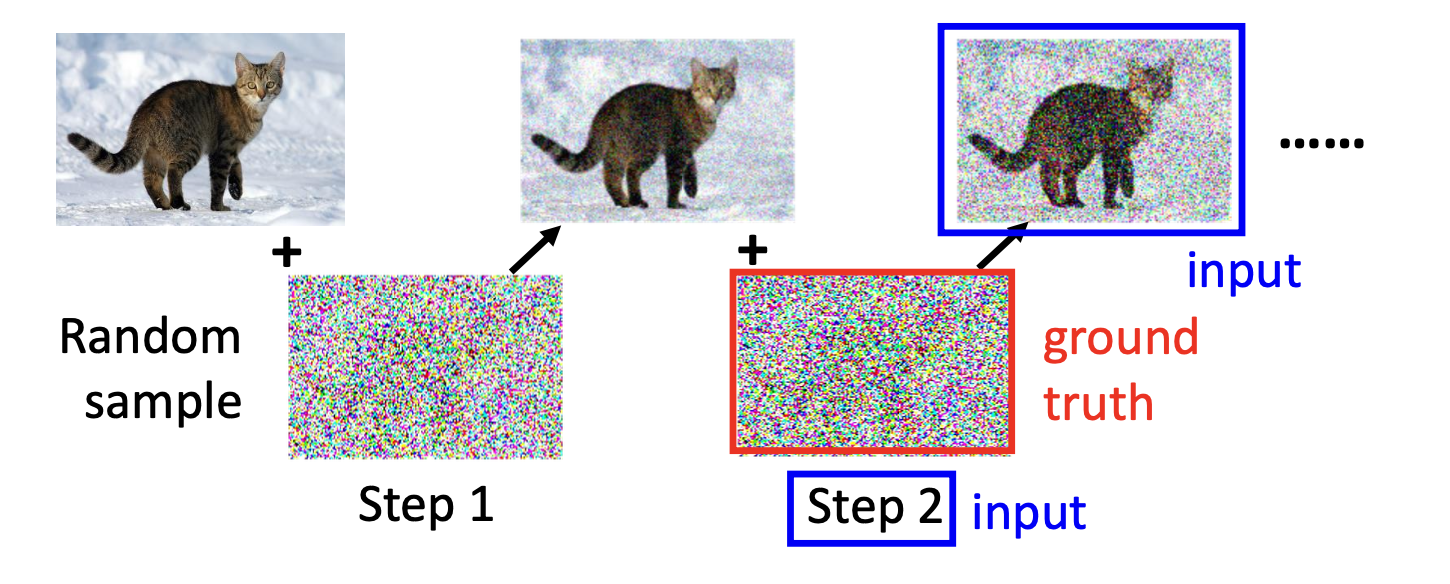
但是实际上，添加噪声是一步到位的。

推导一下这个过程：
$$
\begin{flalign}
&x_1=\sqrt \alpha_1 x_0+\sqrt{1-\alpha_1}\epsilon_1 \
&x_2=\sqrt \alpha_2 x_1+\sqrt{1-\alpha_2}\epsilon_2 \
=&\sqrt \alpha_2(\sqrt \alpha_1 x_0+\sqrt{1-\alpha_1}\epsilon_1)+\sqrt{1-\alpha_2}\epsilon_2 \
=&\sqrt{\alpha_2\alpha_1}x_0+\sqrt{\alpha_2(1-\alpha_1)}\epsilon_1+\sqrt{1-\alpha_2}\epsilon_2 \
=&\sqrt{\alpha_2\alpha_1}x_0+\sqrt{1-\alpha_2\alpha_1}\epsilon_3&
\end{flalign}
$$
从(5)->(6)的原因是：由于$\epsilon\sim\mathcal N(0,1)$，$\epsilon_2, \epsilon_2$是独立的，正态分布的公式，(5)后面两个噪声：
$$
\begin{flalign}
&\epsilon_1^{‘}\sim \mathcal N(0,\alpha_2-\alpha_1\alpha_2) \
&\epsilon_2^{‘}\sim \mathcal N(0,1-\alpha_2)
\end{flalign}
$$
由于正态分布的可加性，所以我们可以直接将这两项合并：
$$
\epsilon_3^{‘}\sim \mathcal N(0, 1-\alpha_1\alpha_2)
$$
于是可以将系数提出来，直接从标准正态分布中采样即可。

为了便于书写，将：$\alpha_1\alpha_2…\alpha_t=\bar \alpha_t$

生成模型的目标

生成模型的目标：

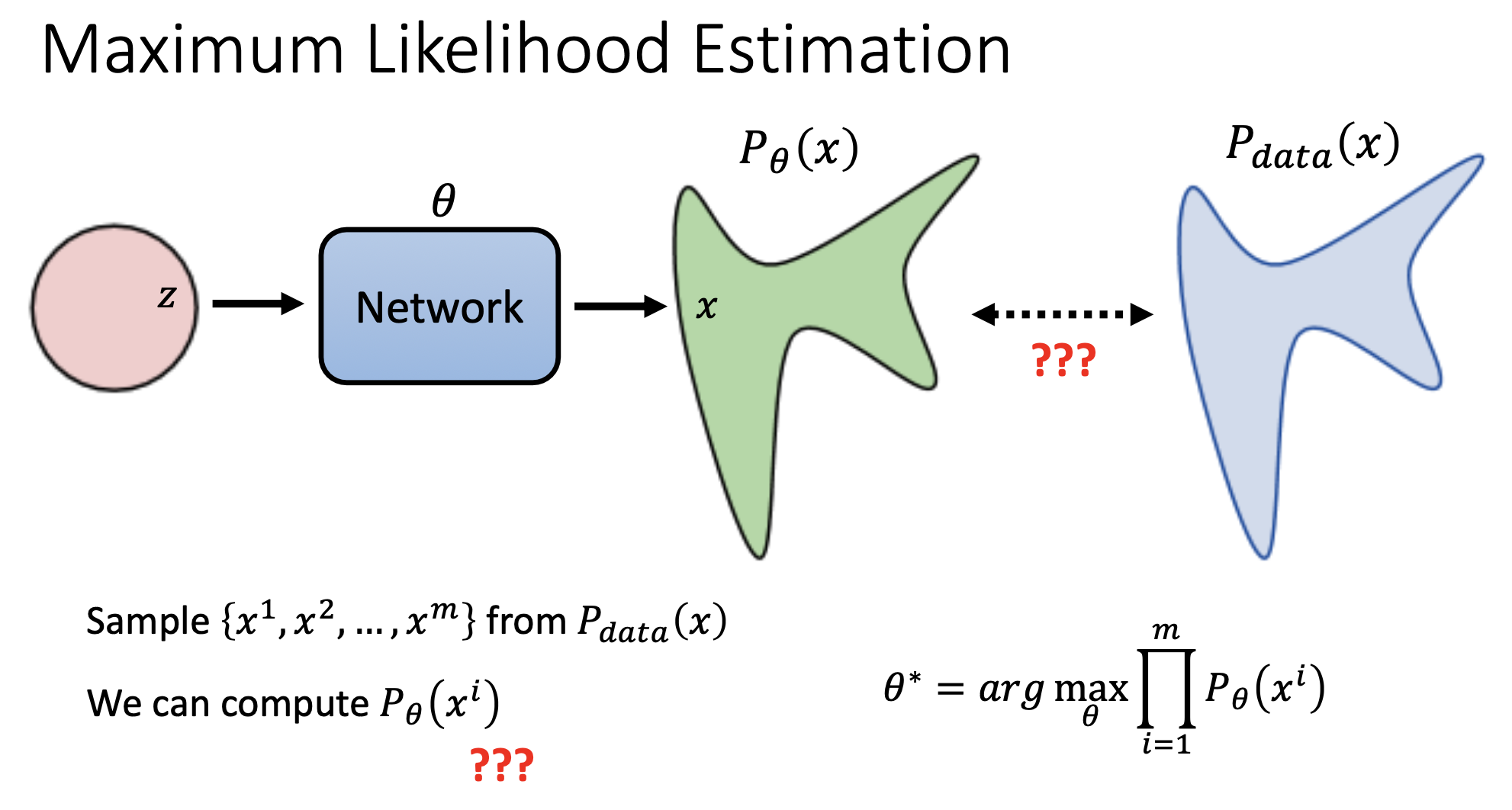
通过NN生成的分布和真实世界的分布一样，将概率分布展开，更容易理解。
$$
P_\theta(x)=\int_zP_\theta(x|z)P(z)dz
$$
目标就是最大化从$P_{data}$中sample出的m个样本的概率$P_\theta$的乘积。

这里补充KL散度的定义，也就是信息论中的相对熵：
$$
D_{KL}(P\Vert Q)=\int p(x)\ln(\frac{p(x)}{q(x)})dx
$$
因此，上述推导的结论是：要想两个分布相近，通过极大似然估计，推导出的结果是最小化两个分布的KL散度。

VAE计算$P_\theta$的方法

上面说到$P_\theta(x)=\int_zP(z)P_\theta(x\vert z)dz$，我们讨论的是生成模型的通用形式，从手上的初始分布中采样一个$z$​，这个概率是已知的。

VAE中的做法是：

输入是x，通过一个encoder，得到latent z。

也就是说，要得到$\theta^*$，就要计算出：在假定x已知的情况下，从z的分布$q()$中采样，求出$\log(\frac{q(x\vert z)}{P(z\vert x)})$的期望的最大值。

DDPM计算$P_\theta$

和VAE的推导比较类似，得到的结论也有相似的结构。

怎么最大化这个期望，这篇paper专门进行推导的，我们直接看结论。

目标的下界是：

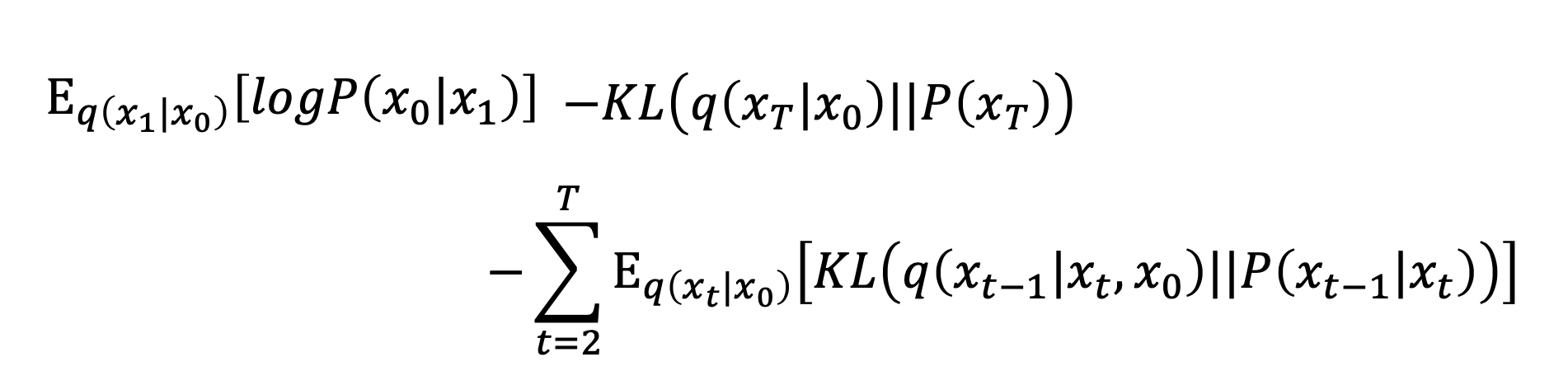
1. 第二项是常数，可以不用管（$q(x_T\vert x_0)$是扩散过程，人为控制；$P(x_T)$是从正态分布中采样一个初始的噪声，也是人为控制，没有$\theta$）。

2. 第三项中，$P_\theta(x_{t-1}\vert x_t)$是逆扩散过程，是由神经网络决定的，而$q(x_{t-1}\vert x_t,x_0)$：
   $$
   \begin{flalign}
   &q(x_{t-1}\vert x_t,x_0) \
   =&\frac{q(x_{t-1},x_t,x_0)}{q(x_t,x_0)} \
   =&\frac{q(x_0)q(x_{t-1}\vert x_0)q(x_t\vert x_{t-1})}{q(x_0)q(x_t\vert x_0)} \
   =&\frac{q(x_{t-1}\vert x_0)q(x_t\vert x_{t-1})}{q(x_t\vert x_0)}&
   \end{flalign}
   $$
   这三项都是可以计算的高斯分布，另一篇paper中推导了这个算式最后得到的是一个什么样的分布：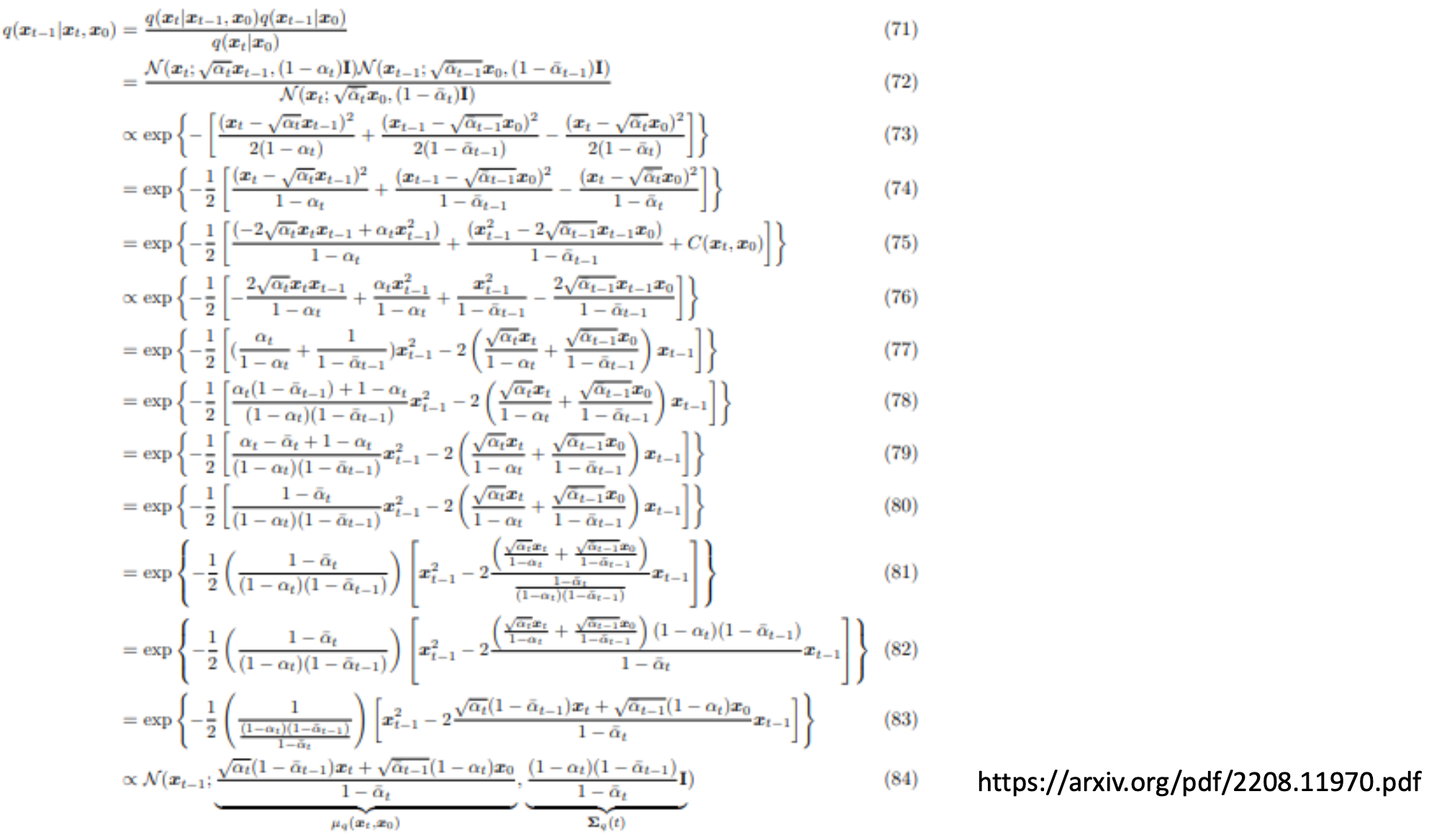

   

   得到了这个分布的均值和方差：

   

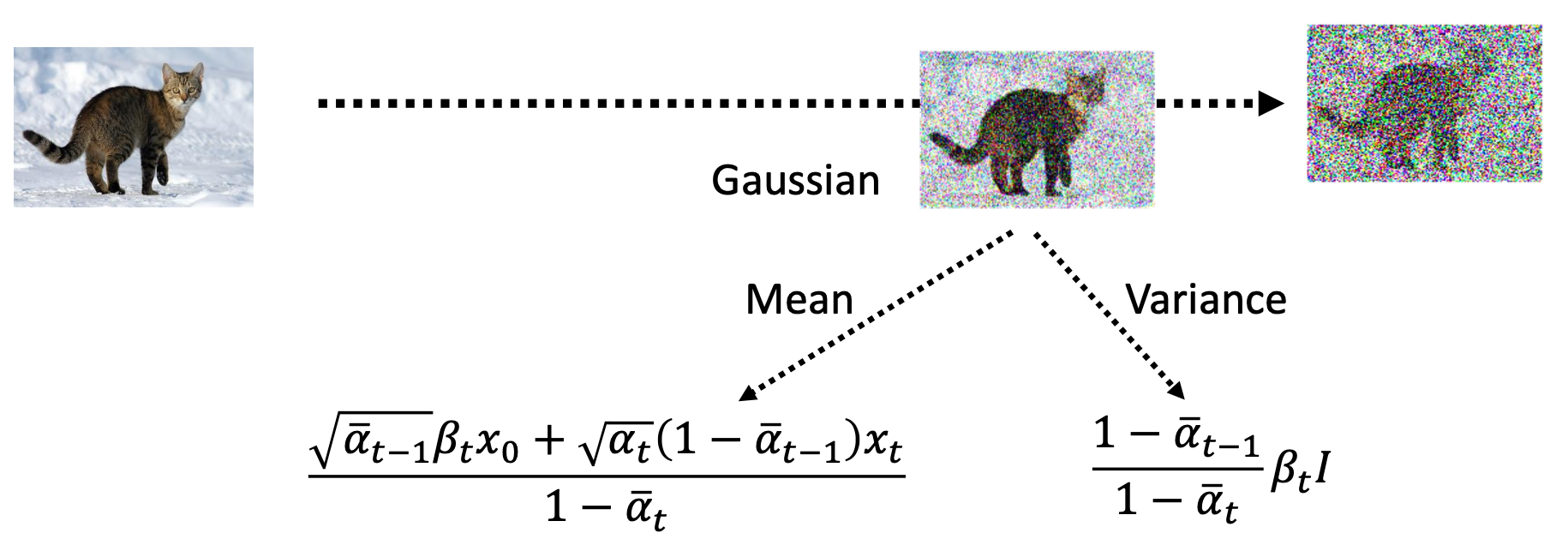
   那么怎么最小化这两个分布的KL散度：
   $$
   KL(p,q)=\log \frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2}{\sigma_2^2}+\frac{(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2}
   $$
   不用直接带入，根据实验，直接最小化这两个分布的均值的距离即可。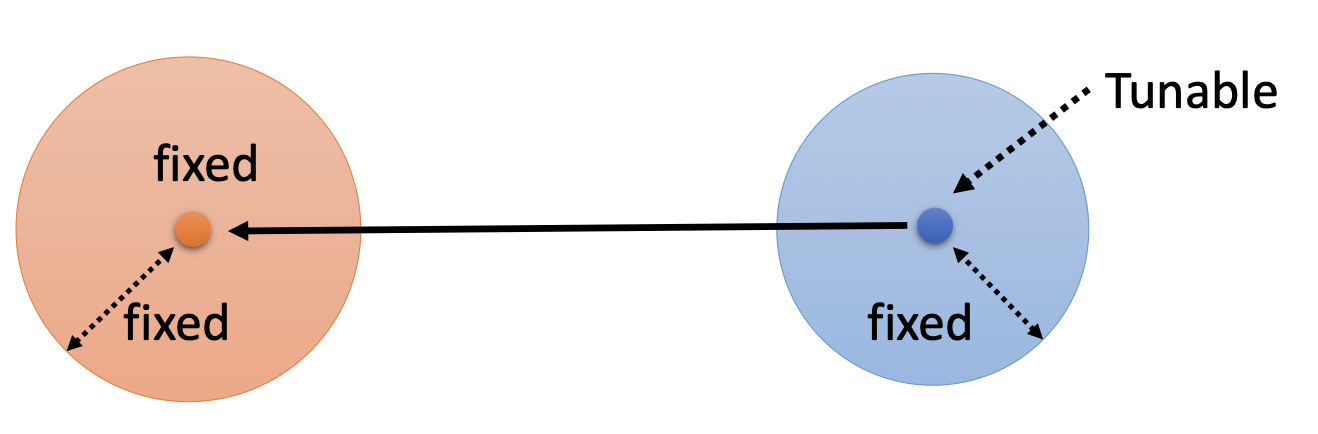

   

3. 第一项参考别人的博客，是这样解释的：

   

最后，$q(x_{t-1}\vert x_t,x_0)$分布的均值，就是diffusion model输出的结果（$x_t$减去predicted noice）：

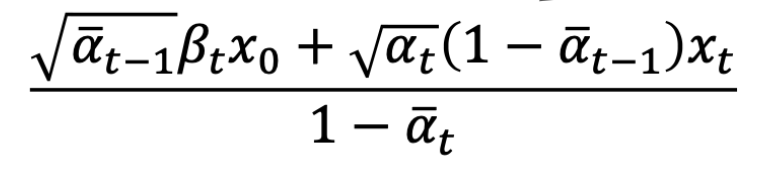
将$x_0$换成$x_t$，得到的就是DDPM演算法中的sample的式子：

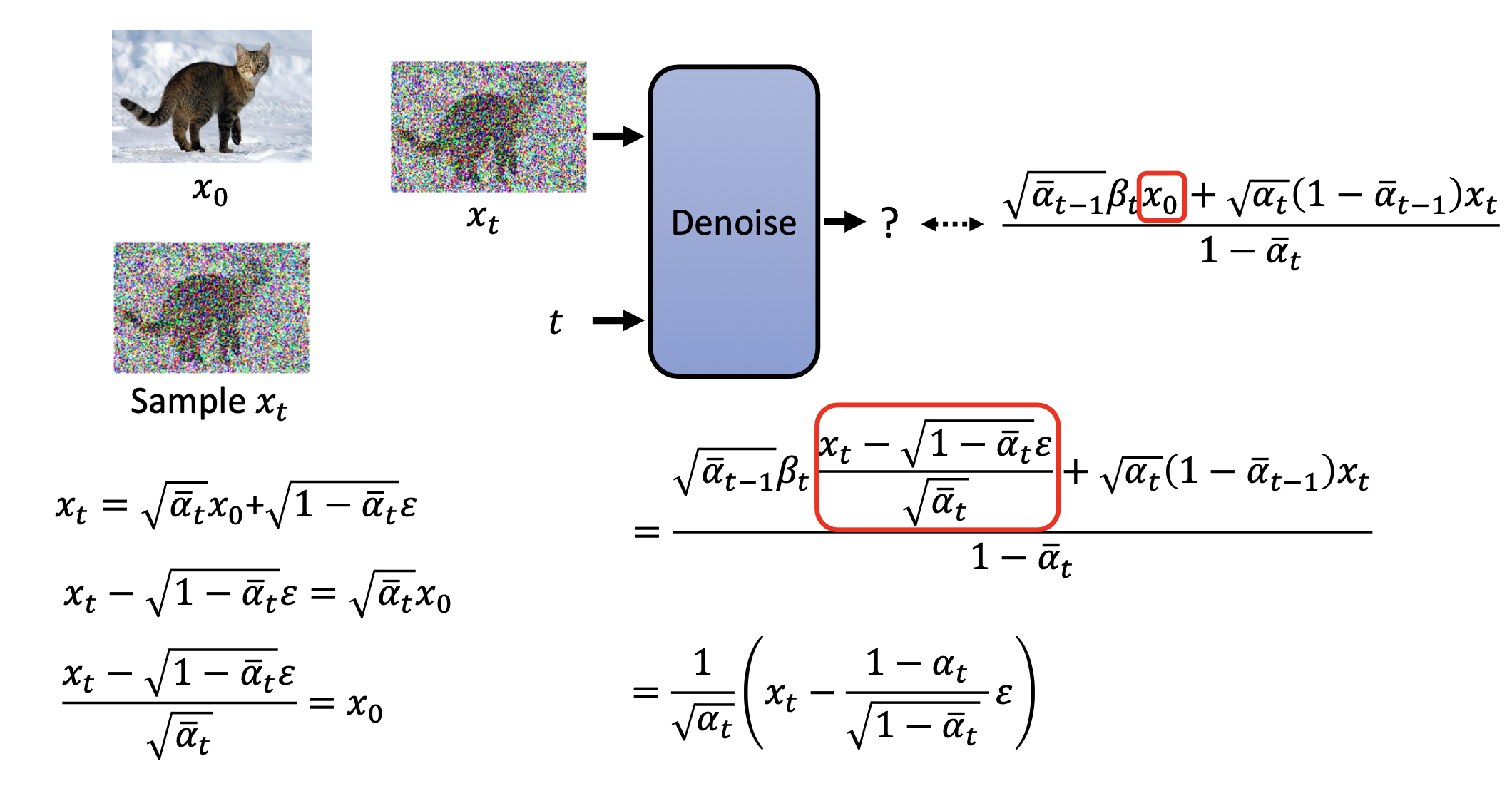
总结DDPM

1. DDPM的出发点和大多数生成模型一样，目标是使得预测的数据分布$P_\theta$和真实世界的数据分布$P_{data}$​一致，以此出发，通过极大似然估计，发现其实等价于最小化两个分布$P_\theta$和$P_{data}$​之间的KL。

   然后有一个比较直觉的式子：
   $$
   P_\theta(x\vert z)\propto \exp (-\Vert G(z)-x\Vert_2)
   $$
   此时目标变成了最大化$P_\theta(x)$

2. 问题在于如何计算$P_\theta$：
   $$
   P_\theta(x)=\int_z q(z\vert x)p(x)dz
   $$
   可以写成上面的形式，用VAE的推导，取对数，得到下界，用来近似$P_\theta(x)\ge E_{q(z\vert x)}(\frac{P(x,z)}{q(z\vert x)})$。

   对于DDPM，用同样的方法，可以推导出相似的结构，$P_\theta(x)\ge E_{q(x_1:x_t|x_0)}(\frac{P(x_0:x_t)}{q(x_1:x_t\vert x_0)})$​

   对于不等号右边的部分，通过大量推导得到下面的式子：

   

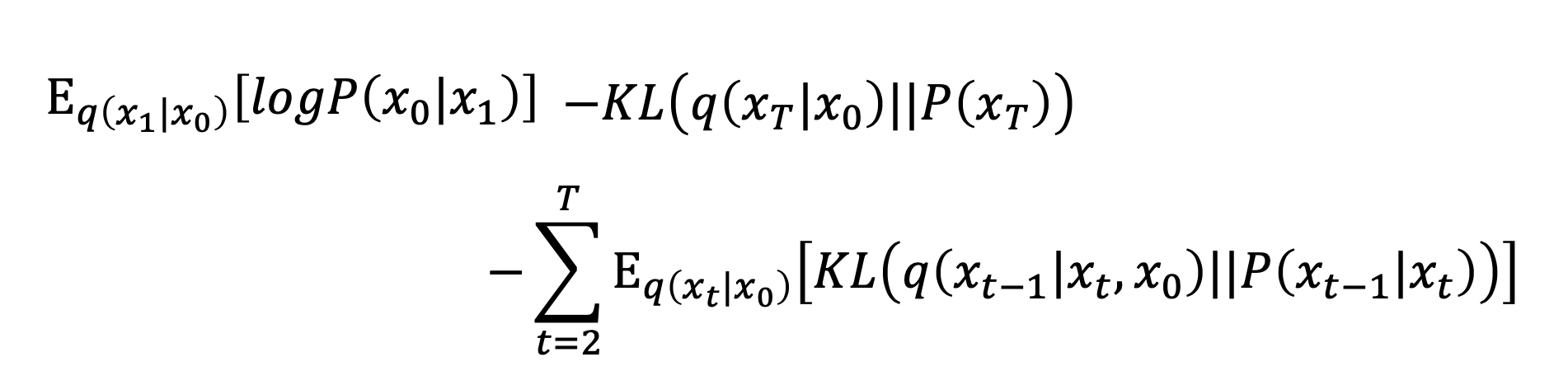
   此时问题变成了最小化第三个KL项了，也就是说那两个分布的均值越接近越好。

参考

DDPM解读（一）| 数学基础，扩散与逆扩散过程和训练推理方法 - 知乎 (zhihu.com)

[PowerPoint 簡報 (ntu.edu.tw)](https://speech.ee.ntu.edu.tw/~hylee/ml/ml2023-course-data/DDPM (v7).pdf)