论文阅读

NIPS2023

摘要

  1. 对原始图片使用一个线性变换，来摧毁后门模式。
  2. 使用扩散模型对变换后的图片进行恢复。

概述

整体的架构

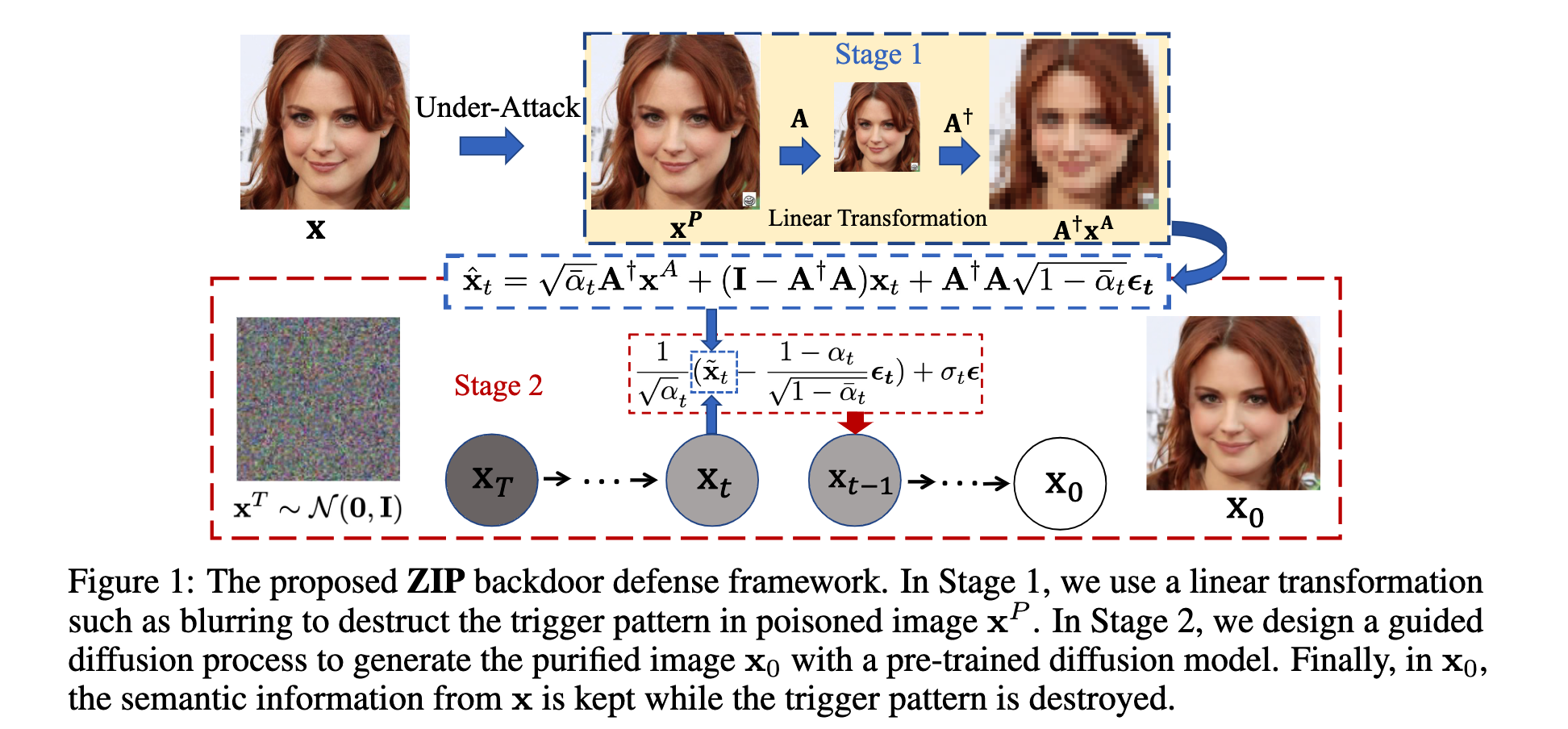
image-20240318132942587

扩散模型

介绍了一种扩散模型DDPM，可以生成高质量的图片，有两个过程：前向过程（forward process）和反向过程（reverse process）:

  • fp：对原始图像$x_0$迭代的不断添加高斯噪声，直到其变为随机高斯噪声$x_T$​

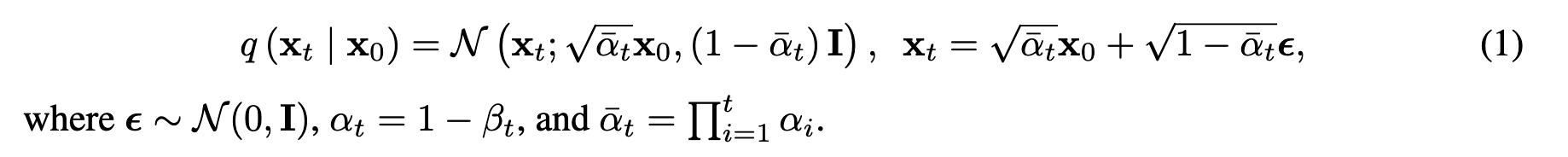
    image-20240318135002113

  • rp：移除随机高斯噪声$x_T$​上的噪声，直到其恢复成原始图像。

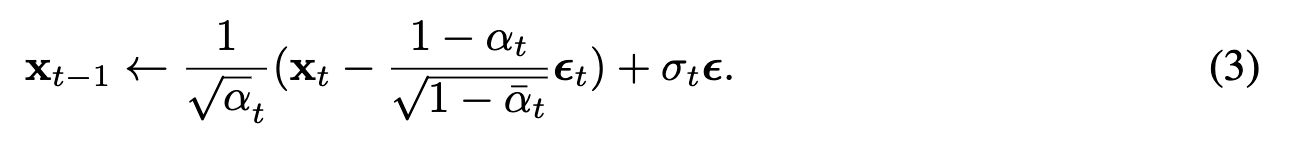
    image-20240318135154622

ZIP

Zero-shot Image Purification(ZIP)的步骤。

  1. 通过线性变换来对原始图像进行模糊。
  2. 通过加以限制的扩散模型对模糊后的图像进行信息恢复。

不能直接用模糊后的图像来进行分类，由于损失了太多信息，这样会导致准确率低。

图像变换和分解

通过下式对图像进行变换：
$$
x^A=Ax^P=A(x+p)
$$

  • $x^A$：经过线性变换模糊后的图像
  • $A$：线性变换
  • $x$：原始图像
  • $p$：触发器，毒化数据

理想的经过扩散模型恢复的图片$x_0$应该具备以下特性：
$$
A(x_0+p)=A(x+p)=x^A
$$
将图片x进行分解：
$$
x=A^{\dagger}Ax+(I-A^{\dagger}A)x
$$
称左边这一部分为范围空间中的观测，而右边这一部分则是零空间中的观测。

于是：
$$
(x_0+p)=A^{\dagger}A(x_0+p)+(I-A^{\dagger}A)(x_0+p)
$$
得出：
$$
x_0=A^{\dagger}x^A-A^\dagger Ap+(I-A^\dagger A)x_0
$$
(5)则是理想的恢复后的图像组成表示，前两部分是范围空间的中的观测，最后一部分是零空间中的观测。但死零空间中的信息是不可观测的。

用扩散模型来进行图像净化

通过扩散模型的前向过程，和上面的公式(5)，可以得出：

image-20240318194853919

$\epsilon_t$是由扩散模型$g_\phi$生成的噪声，$\epsilon _t=g_\phi (x_t,t)$，$x_t^{‘}$是$x_t$的估计。

然后再用扩散模型的反向过程对$x_t$进行迭代：

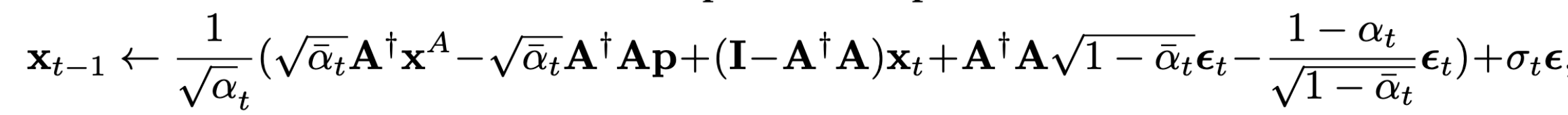
image-20240318195448130

将反向过程适配到零样本适配

由于防御者不知道触发器$p$，因此，选择忽略中间带有$p$的一项，并用$\hat x_t$来估计$x_t^{‘}$

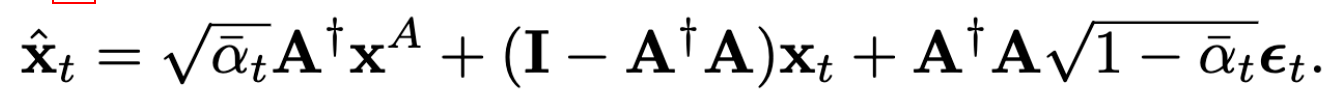
image-20240318200936982

选择忽略$\sqrt{\bar \alpha _t}A^\dagger Ap$的原因还有：

  • $\sqrt {\bar \alpha _t}$刚开始很小。
  • 由于后门攻击的隐蔽性，所以p也很小

由于是迭代，这样进行近似可能会带来指数级别的误差，因此，作者采取将每一次迭代的近似误差限制在一个范围内，确保最后恢复出的图像能够在模糊触发器的同时，保留原始图片的关键信息。

假设：
$$
g_\phi (x_t,t)=\epsilon _t
$$
那么：
$$
g_\phi ((x_t+\sqrt{\bar \alpha _t}A^\dagger Ap), t)=\epsilon _t+\epsilon_t^{‘}
$$
通过推导可以得到误差的边界：

image-20240319141055709