第一章

子空间

  • 加法
  • 数乘
  • 取值证明子空间非空

线性变换

  1. 证明线性变换
    • 加法
    • 数乘
  2. 求线性变换T在基E下的矩阵
    • 求出$T(E_1)=(E_1,E_2,E_3)(x_1,x_2,x_3)^T$
    • 将x的向量拼起来，得到矩阵

第二章

内积

  1. 证明内积

    验证：

    • $(\alpha,\beta)=(\beta,\alpha)$
    • $(k\alpha,\beta)=k(\alpha,\beta)$
    • $(\alpha+\beta,\gamma)=(\alpha,\gamma)+(\beta,\gamma)$
    • $(\alpha,\alpha)\ge0$

  2. 求标准正交基

    • 最终都可以化成矩阵，例如：

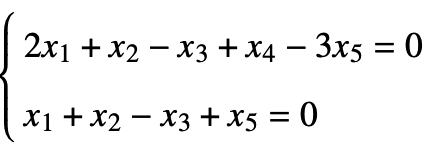
      image-20231230101957379

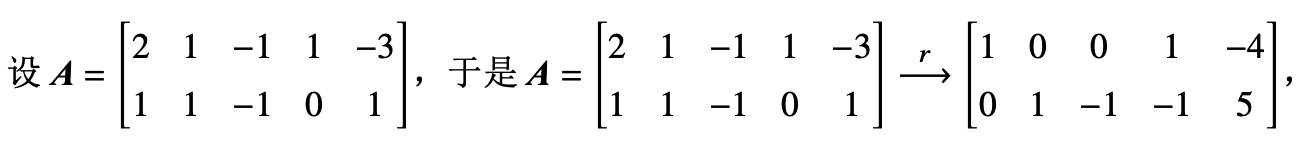
      image-20231230102006811

      把前两个当未知数，后三个依次取100 010 001

      得到三个基。

    • 正交化

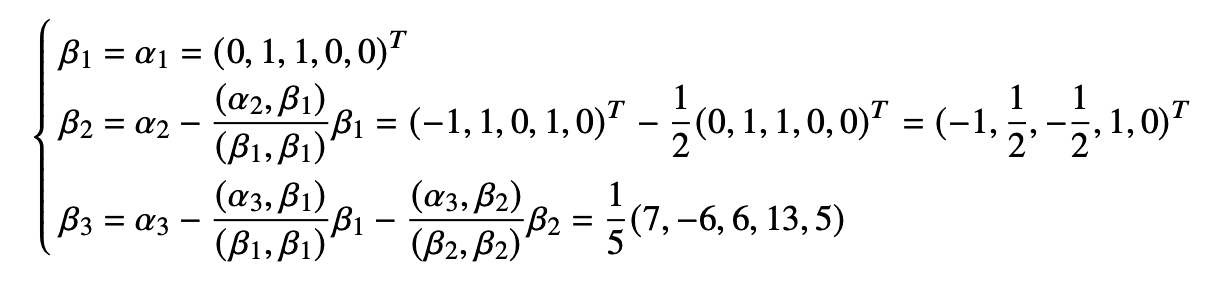
      image-20231230102307464

    • 单位化

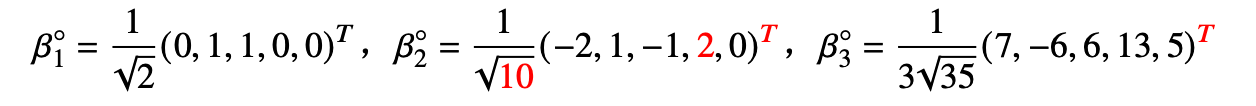
      image-20231230102330894

第三章

约旦标准型

  • 求出行列式因子$D_1,D_2,D_3$
  • 求不变因子$d_1,d_2,d_3$
  • 求初等因子
  • 写Jordan块

最小多项式

  • 求特征多项式

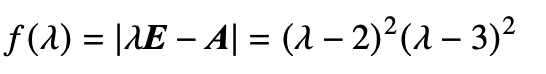
    image-20231230114208265

  • 所有可能的最小多项式

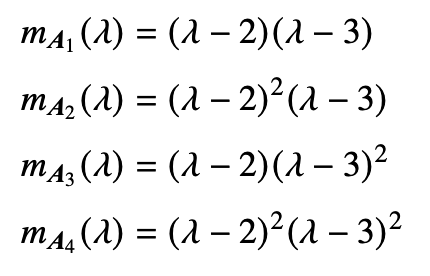
    image-20231230114230409

  • 验证：把$\lambda$换成A，数字换成E，哪个为0矩阵，就是最小多项式

第四章

LU分解

将(A,E)进行初等变换，直到A变成了上三角矩阵，那么左边就是U，右边是L的逆矩阵，求逆得到L

image-20240102151627607

QR分解

方针的QR分解如下：

image-20240102153251242

image-20240102153301164

对于非方阵，需要使用施密特正交化：

image-20240104202323908

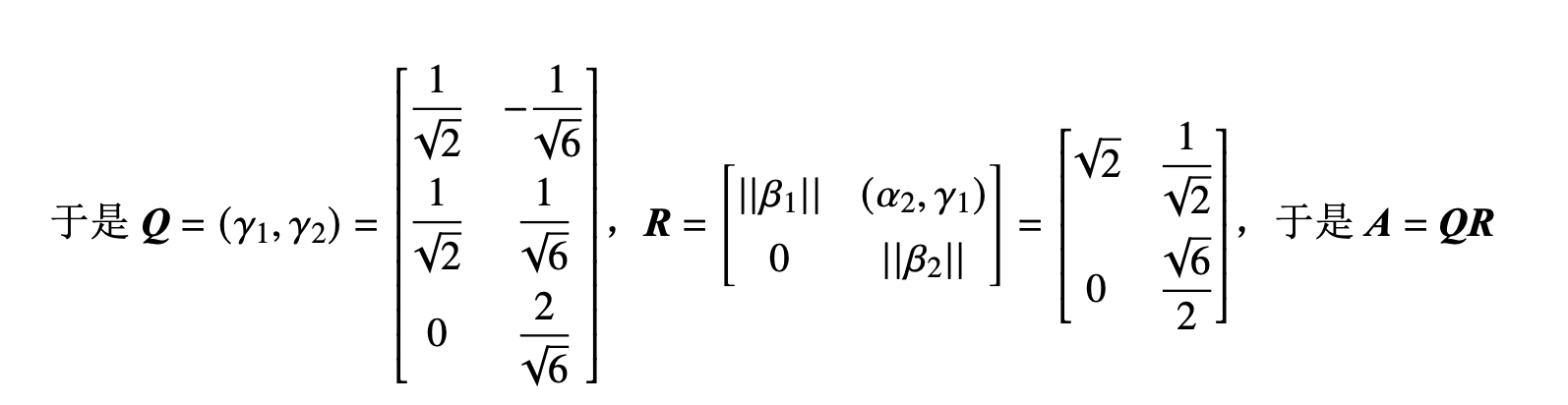
image-20240104202332599

满秩分解

image-20240102162204976

C取得是初等变换后，除掉0行后剩下的矩阵

B取得是初等变换后得到的行最简H，”1“所在的列在原矩阵A中的表示。

$A^+$

image-20240102162240251

相容性

若是$AA^+b\ne b$，那么不相容

奇艺值

只需要会算奇艺值即可。

image-20240102162724100

第五章

证明XXX是一种范数，略

常见矩阵范数

image-20240102163944561

image-20240102163957039

总结；

image-20240102164009644

求最小二乘解

先求出$A^+$

然后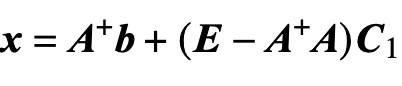image-20240102164106539

极小范数的最小二乘解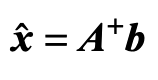：image-20240102164135525

第六章

image-20240107161839651