Graph augmentation
for one graph G, if:
- G is too sparce => MP(message-passing) not efficient
- G is too dense => MP costly
- G is too large => GPU memory not enough
then it is unlikely to use the computational graph as the raw input. $G_{raw}\ne G_{computational}$
Here are some methods to do Graph Augmentation:

feature augmentation
lake feature
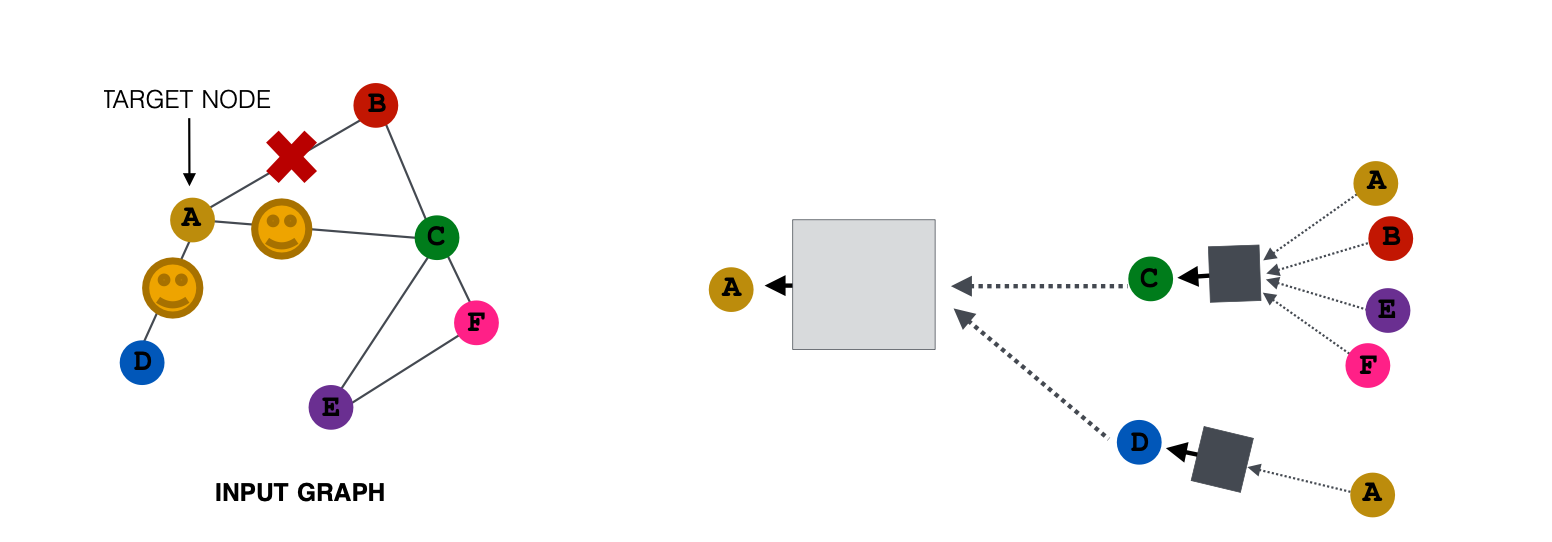
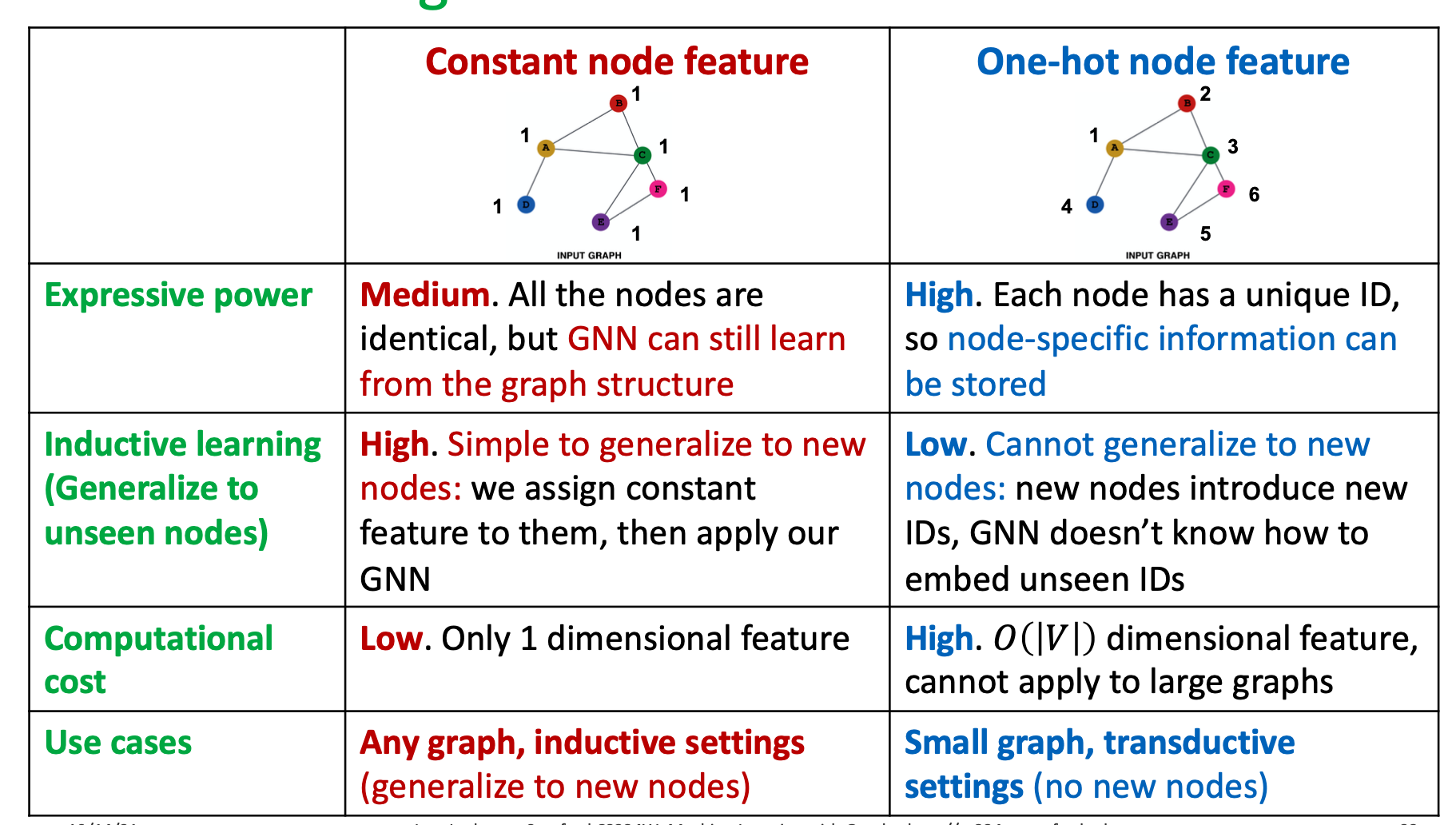
if we only have adj. matrix, the simple methods are:
- assign constant value to nodes(value 1)
- Assign unique IDs to nodes(one-hot encoding)
hard to learn GNNs struct
for example, the GNN can’t capture the cycle length of node v:
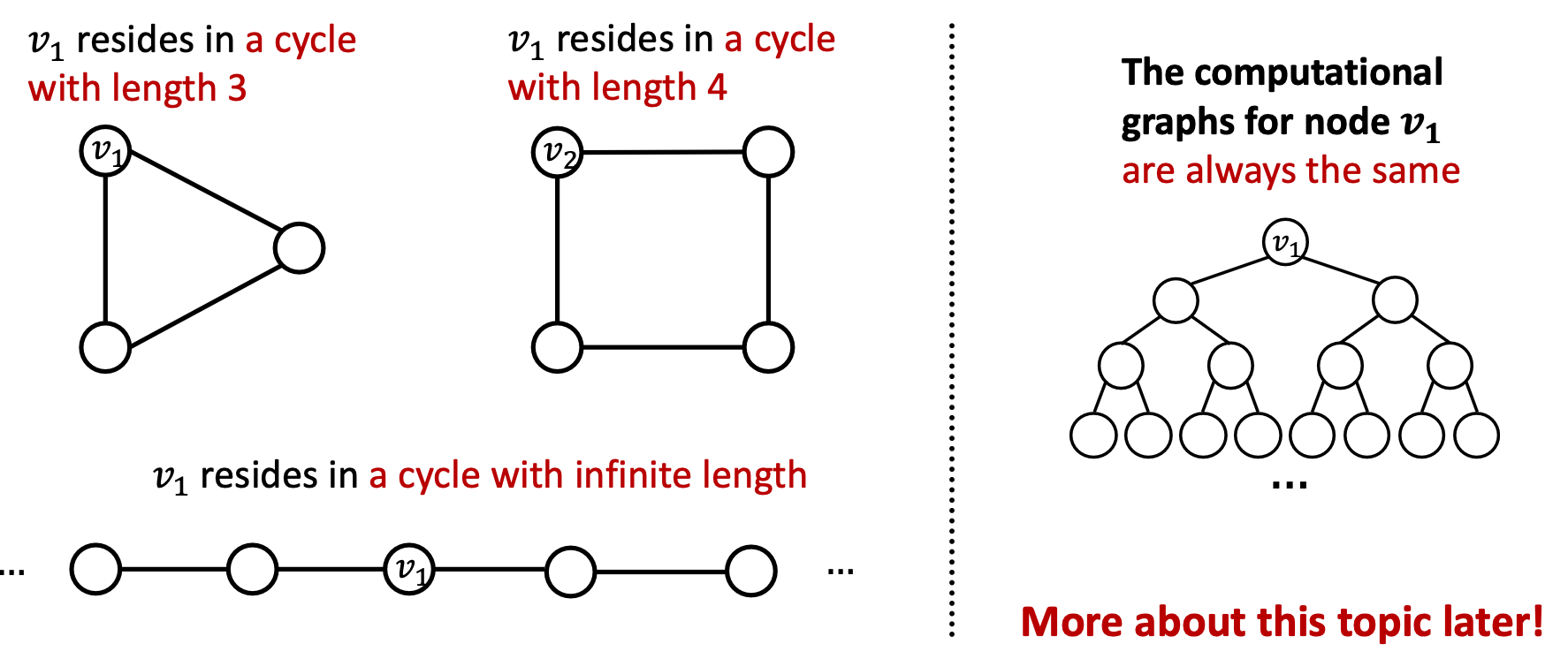
This means: use the graph struct as computational graph is not enough. Nodes cannot learn the graph certain struct.
the solution is: add more network struct frature to node.

these can be seen in ch2 or 3.
struct augmentation
add virtual edges
common approach: use $\mathcal{A}+\mathcal{A}^2$ instead $\mathcal{A}$ as computational graph.
for example, in bipartite graphs:
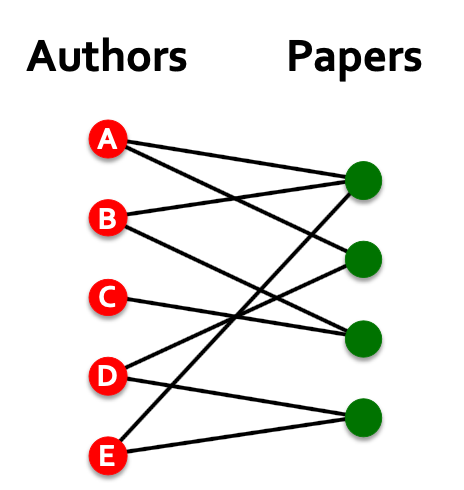
if use $\mathcal{A}+\mathcal{A} ^2$, the 2-hop nodes will be connected, which means we can get a co-authors-paper network or co-paper- author network.
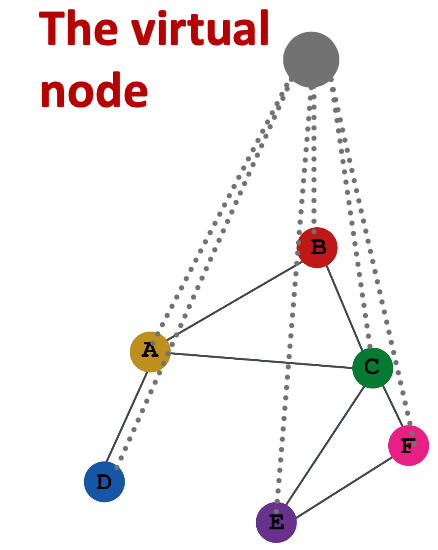
add virtual ndoes
common approach: add a vitual node than connects to all nodes.
if the graph is too sparse, and 2 node distance 10-hops, then the virtual node can improve the message passing.
node neighbor sample
if a node’s degree is too large($10^5 degrees$), then we can sample the most important 1000 or 10000 nodes to converge. And in next epoch, we randomly sample again to increase the robust of model.