in node embedding, we use encoder to map original network node to embedding space, the encoder is:
$$
z_v=Z.v
$$
the matrix is what we need to learn.
now, we use deep learning-based method as our encoder, which is composed of multiple layers of non-linear transformations.

What makes graph representation learning so difficult?
- no fixed graph
- Dynamic and no fixed fratures
Basics of DL
we usually view the task as an Optimization problem, which means we need to min. the objective function(loss function).
for predict task, use L2 loss:
$$
L(y,f(x))=||y-f(x)||_2
$$
or L1 loss.
for classify problem, we use cross entropy(CE)
$$
CE(y,f(x))=-\sum_{i=1}^C(y_i\log f(x)_i)
$$
$$
f(x)=softmax(g(x))
$$
g is the model.
Deep Learning for graph
what if we directly feed the graph adj. matrix and feature set?
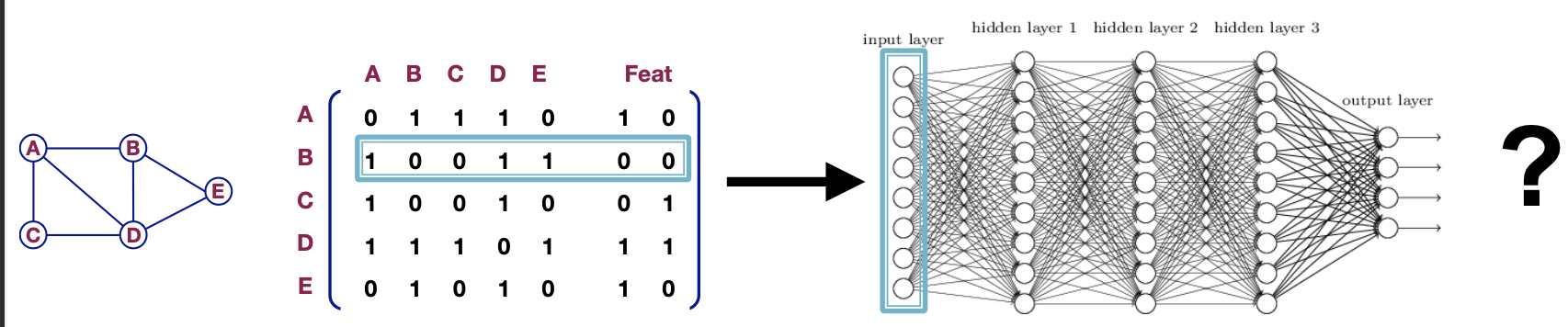
Problem:
- Parameter $O(|V|)$, certainly speaking is $O(|V|+num_{frature})$
- the graph size is fixed
- sensitive to node ordering
what about convolutions?
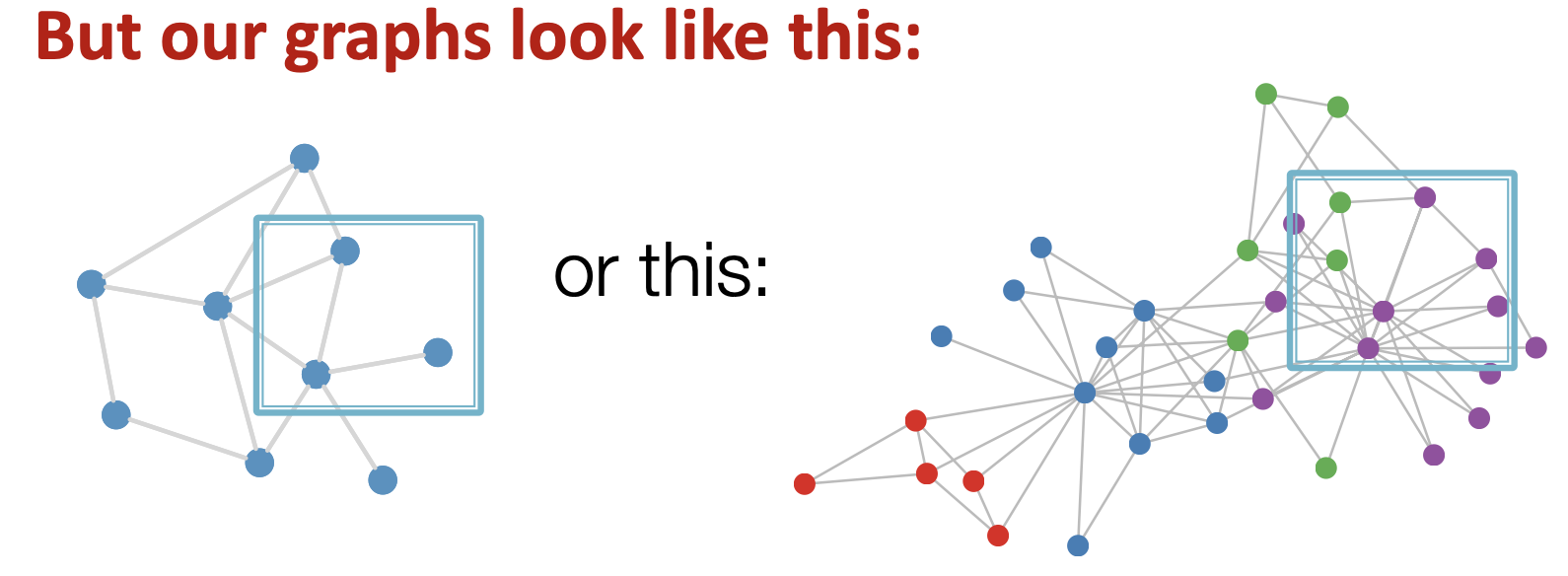
problem:
- no stride or slide
- permutation invariance(改变排序不变性)
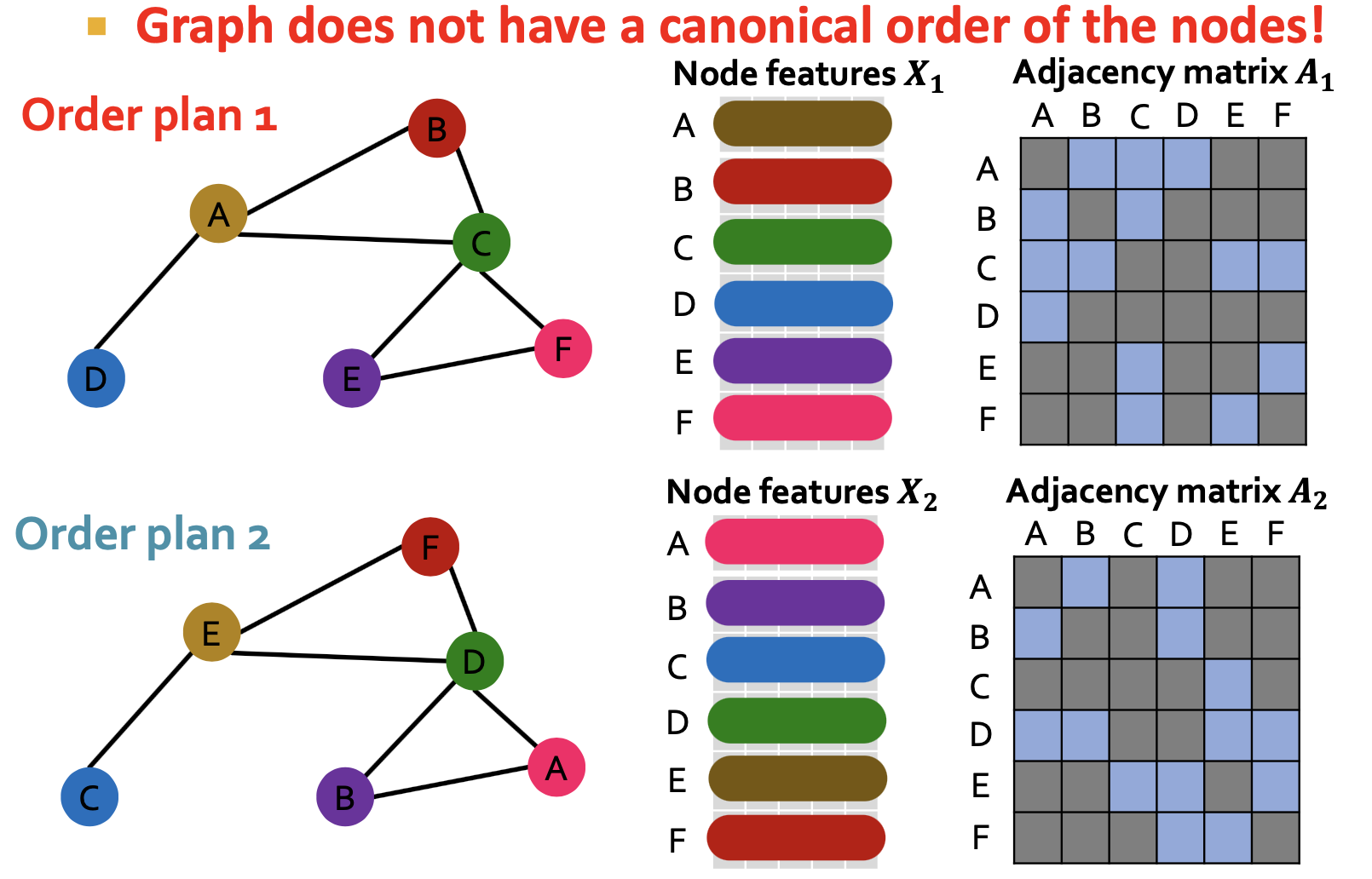
graph and node representation should be the same for plan1 and plan2.
we need a permutation invarient function!
and maps, cons cannot solve this.
Graph Convolutional Networks
main problems are:
too many parameter
order invariance
first we solve proble 1!
Lets consider mlp $\to$ CNN
we use the kernel to share parameter and aggregate information(spacial)
can we apply it to GNN?
idea: for node v, use it as an kernel to aggregate information from $N(v)$, thus, node’s neiborhood defins the computation graph
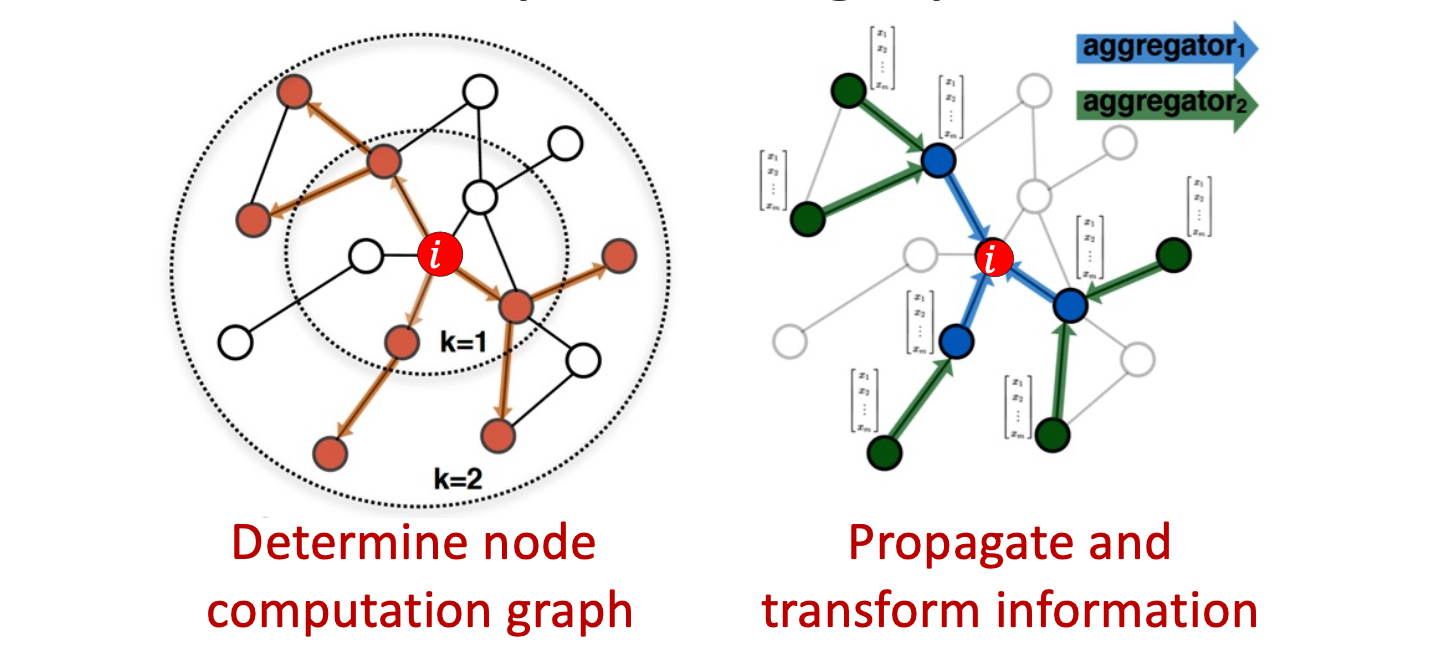
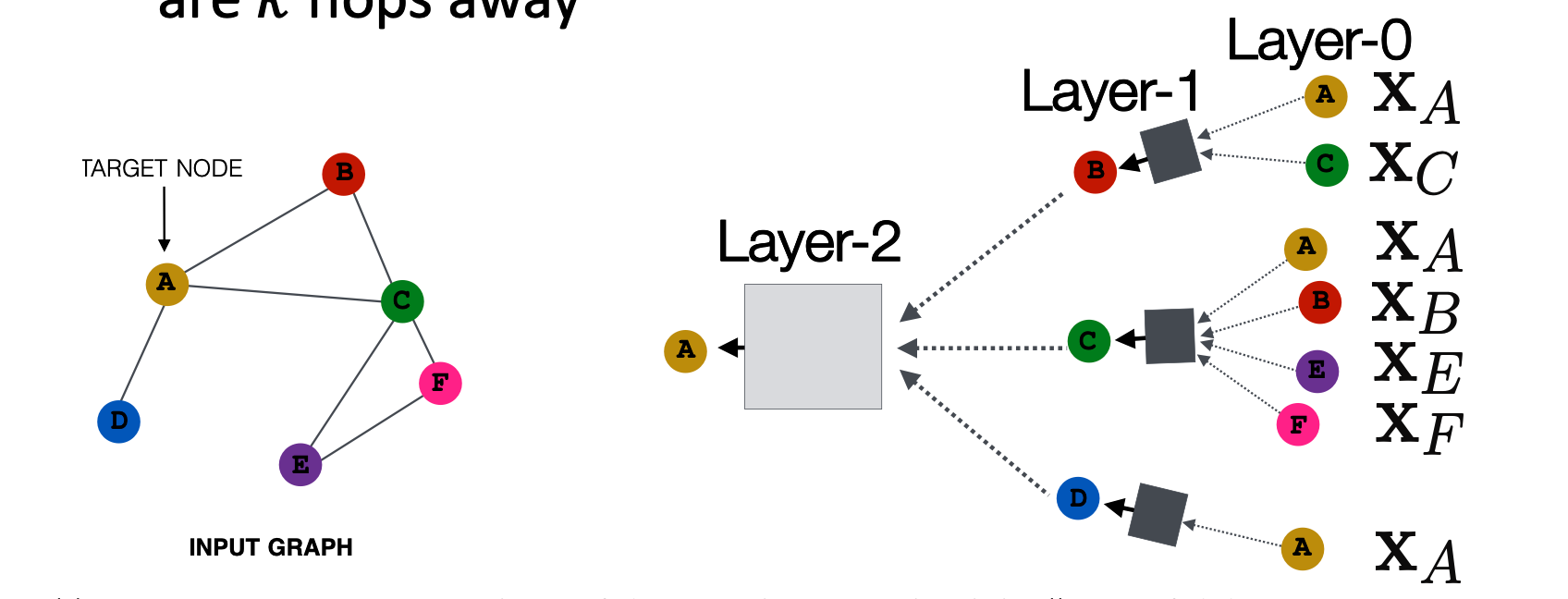
now we solve the prob.1, how to keep order invariance?
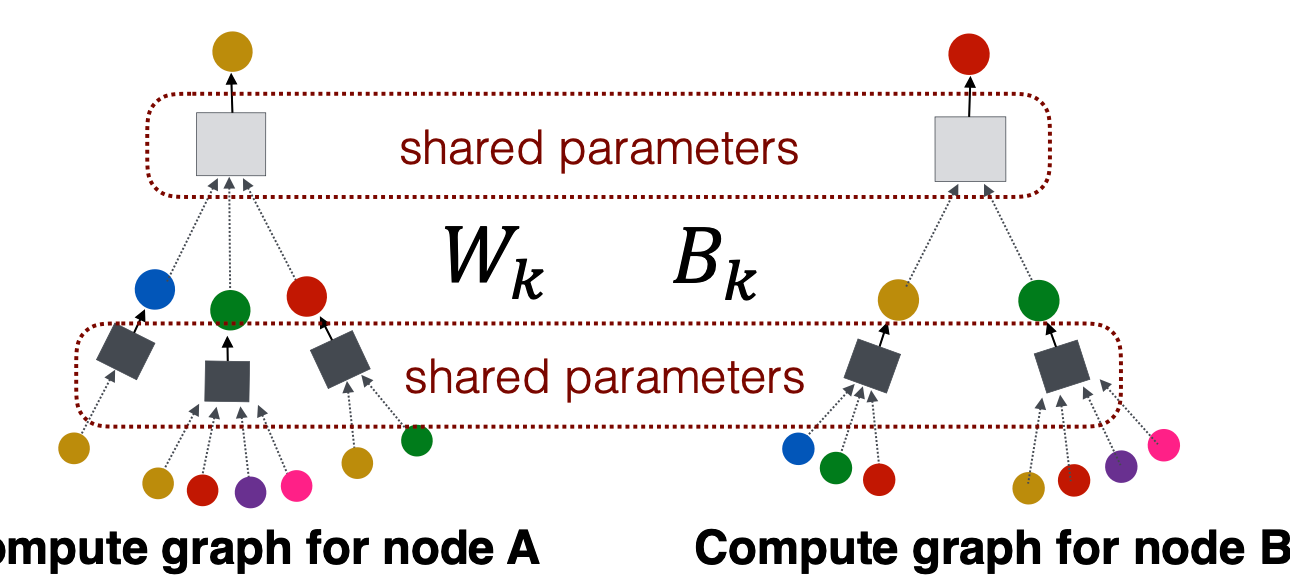
the approach is: Average information from neighbors and apply a neural network
now we can get the formulation of GNN(GCN):
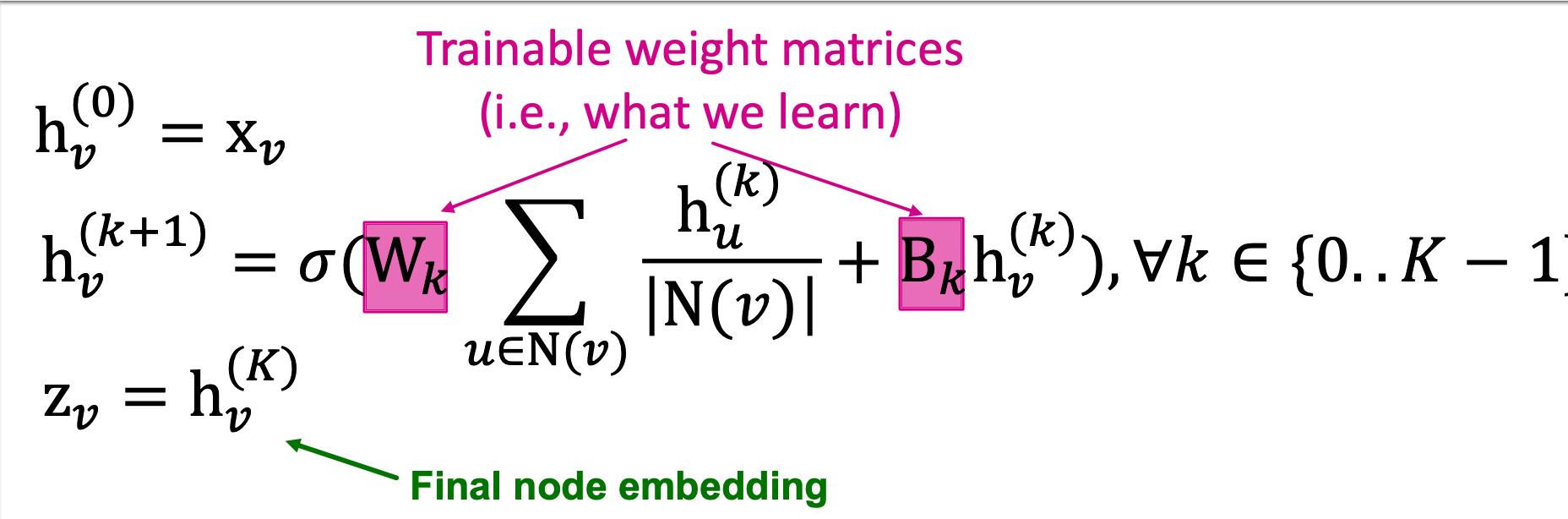
and the matrix formulation:


Train GNN
Supervised learning
$$
\min _{\theta}\mathcal{L}(y,f(z_v))
$$
e.g., drug classification(toxic or not)
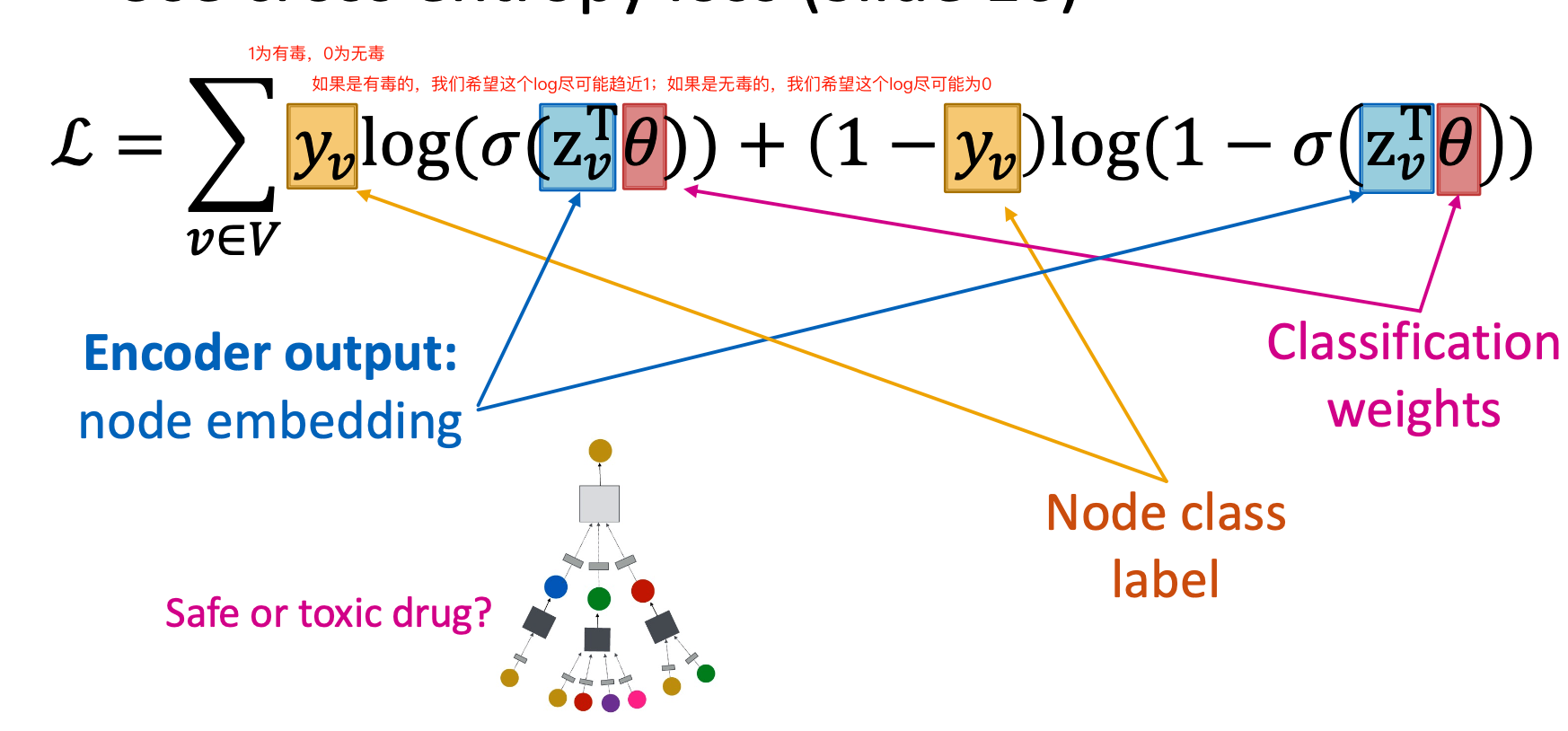
the $f(x_v)$ is $\sigma (z_v^T\theta)$
Unsupervised learning
$$
\mathcal{L}=\sum_{z_u,z_v}CE(y_{u,v},DEC(z_u,z_v))
$$
if node u and v are similar, then $y_{u,v}=1$

