cs224w

PageRank

how to represent page as graph:

  • Node: web pages
  • Edge: hyperlinks

Not only page network, here are citation natwork and reference network:

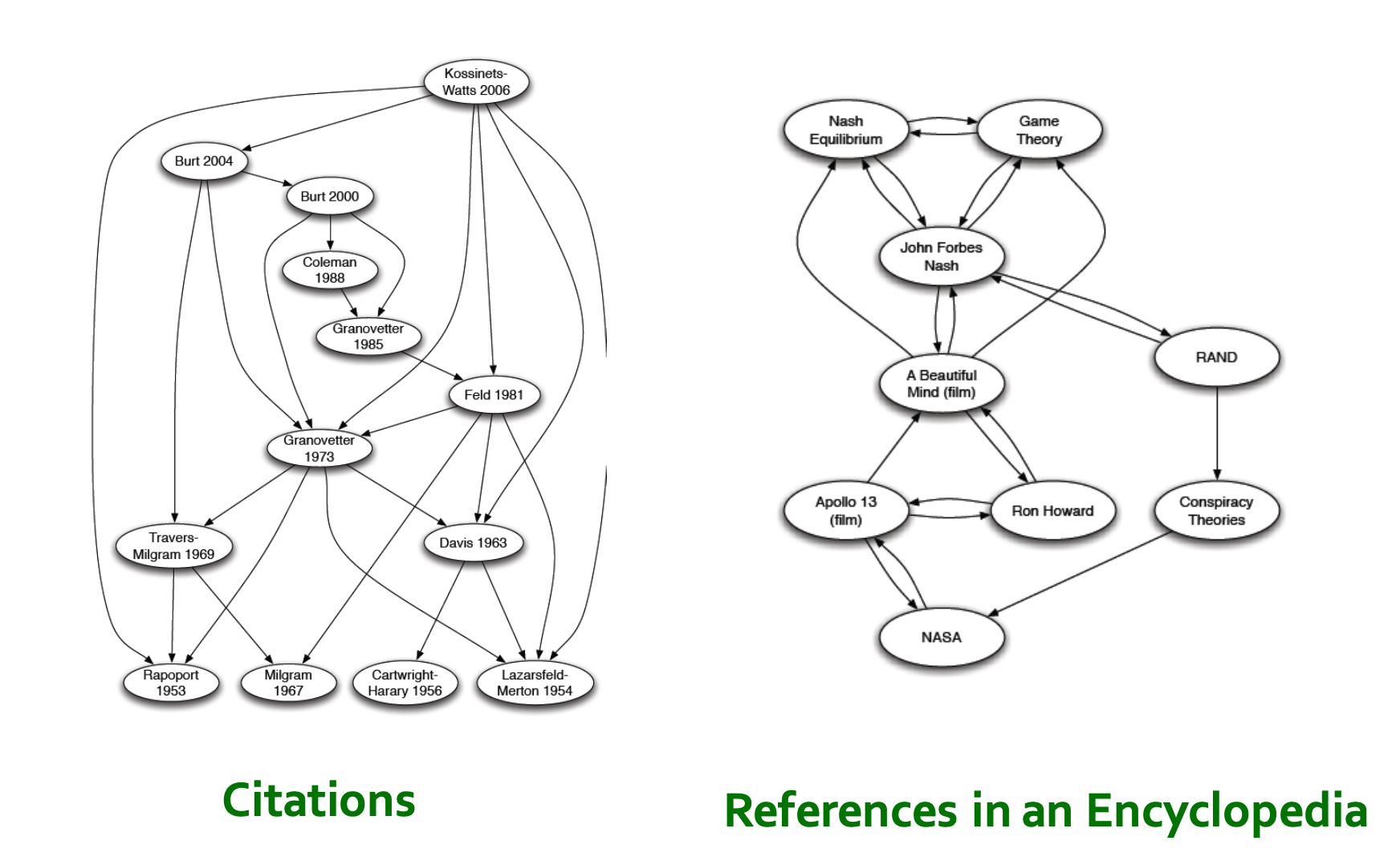
image-20231016105115978

The problem is how could we measure the important of a web page so that we can rank them.

the idea is: links and votes

the intuition is that Page is more important if it has more links

consider 2 web page:

why we don’t consider out-link?

Because in your website, you can set a lot of out-links, and it is easy to implement. So the inportance only take in-link into consideration.

so, what is vote?

image-20231016110419927

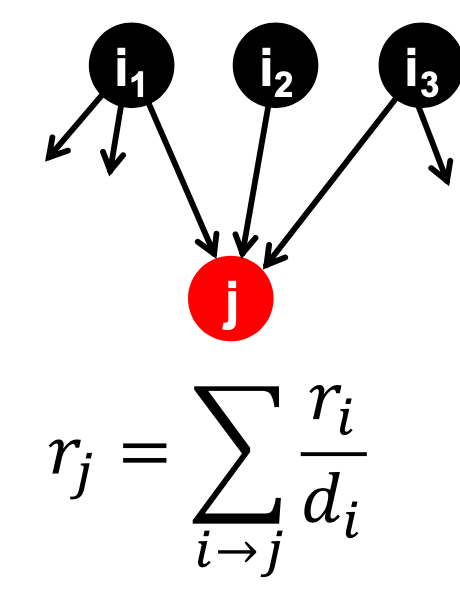
we use in-links to caculate the importance of node j, j have 2 in-links, so it’s importance is above.

And consider other nodes, such as node i, has 3 out-links, so its importance to others is divided to $\frac{r_i}{3}$

for a 3 node graph:

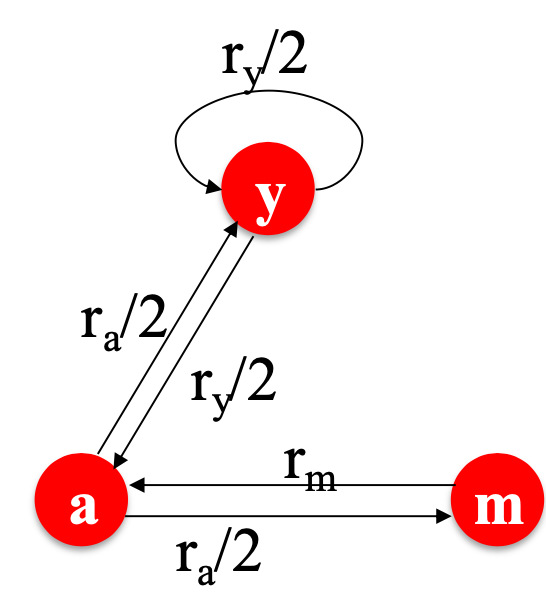
image-20231016110800556

we can get the equation for each node: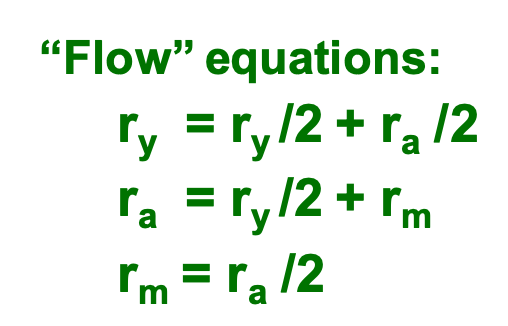
image-20231016110819595

Matrix Formulation

Let us start at some notion.

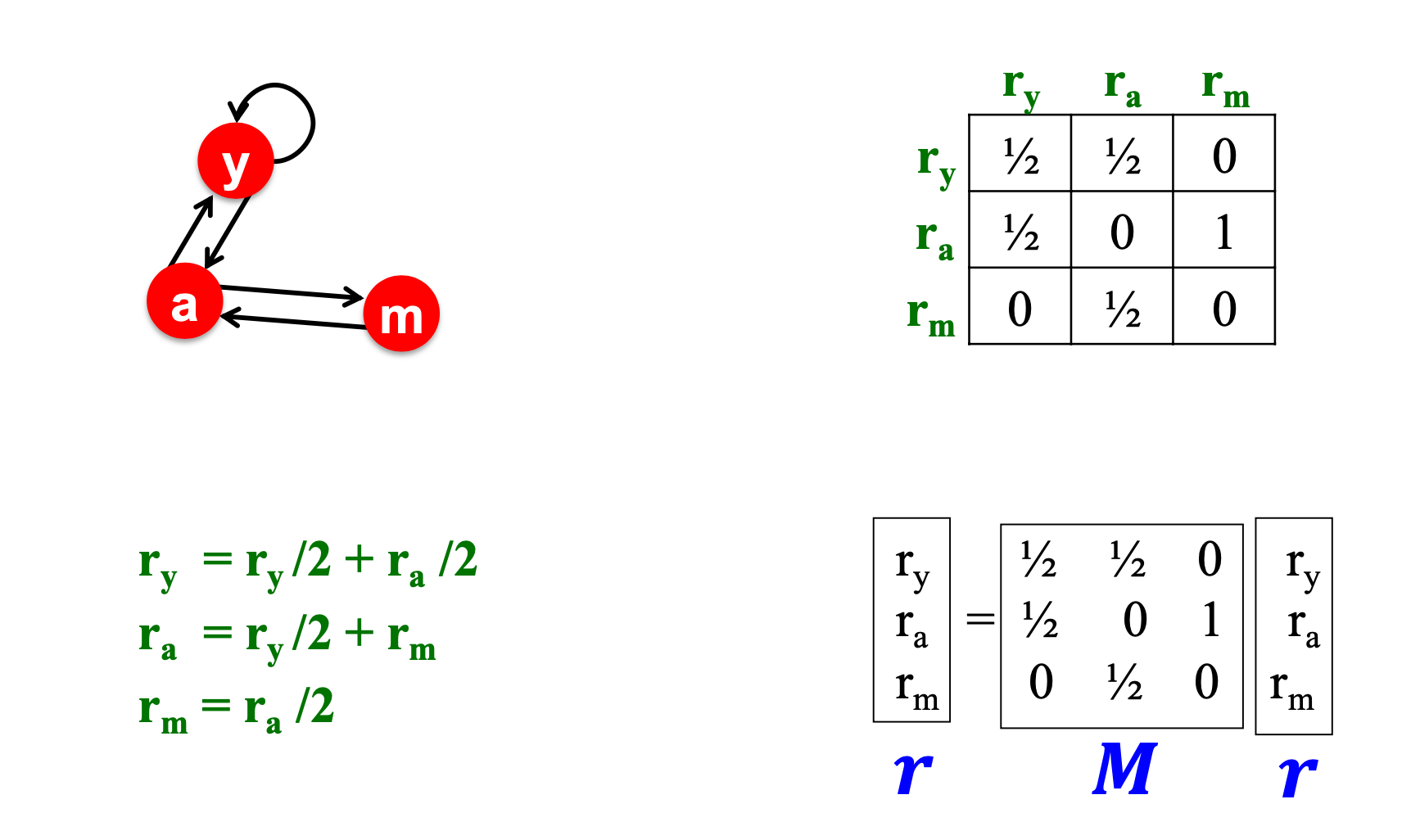
  1. Stochastic adjacency matrix $M$

    Here are the rules:

    • $d_i$ is the out degree of node $i$
    • if $i\to j$, then $M_{ji}=\frac{1}{d_i}$, which means the importance of $i$ is divided and given to $j$

  2. Rank vector $r$

    $r_i$ is the importance of page $i$, and $\sum_ir_i=1$.

and the flow equation can be written as:
$$
r=M.r
$$
image-20231016111626006

Connection to Random walk

we have considered the importance of node. now lets start at one page i, and which page should we select next?

  1. at timepoint t, the surfer is at page i
  2. at timepoint t+1, surfer choose an put-link from i randomly.
  3. the surfer at page j
  4. repeat

image-20231016131736772

so, here are some notions:

  • $p(t)$: the coordinate of the probability of node i at the time t. it includes the next pages probability.
  • $p(t)$ is a probability distribution over pages

this process can be performed as this fomula:
$$
p(t+1)=M.p(t)=p(t)
$$

$$
r=M.r
$$

$r$ is the stationary distribution for random walk

in ch2, the centrality:
$$
\lambda c=Ac
$$
c is eigenvector, $\lambda$ is eigenvalue

so eigenvector is r, eigenvector is 1
$$
1.r=M.r
$$

Solve PageRank

notion and procedure

we have the equation with eigenvalue 1 and eigenvector $r$, and its equal form is:

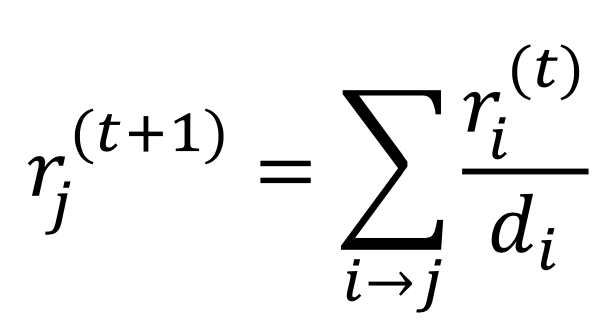
image-20231016144335069

now we use iterative procedure to solve it:

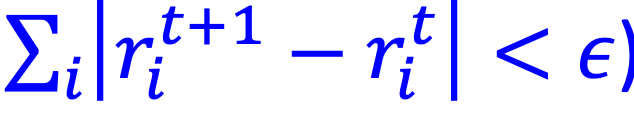
image-20231016144426163

the whole procedure is as follow:

image-20231016144523411

Here are some example:

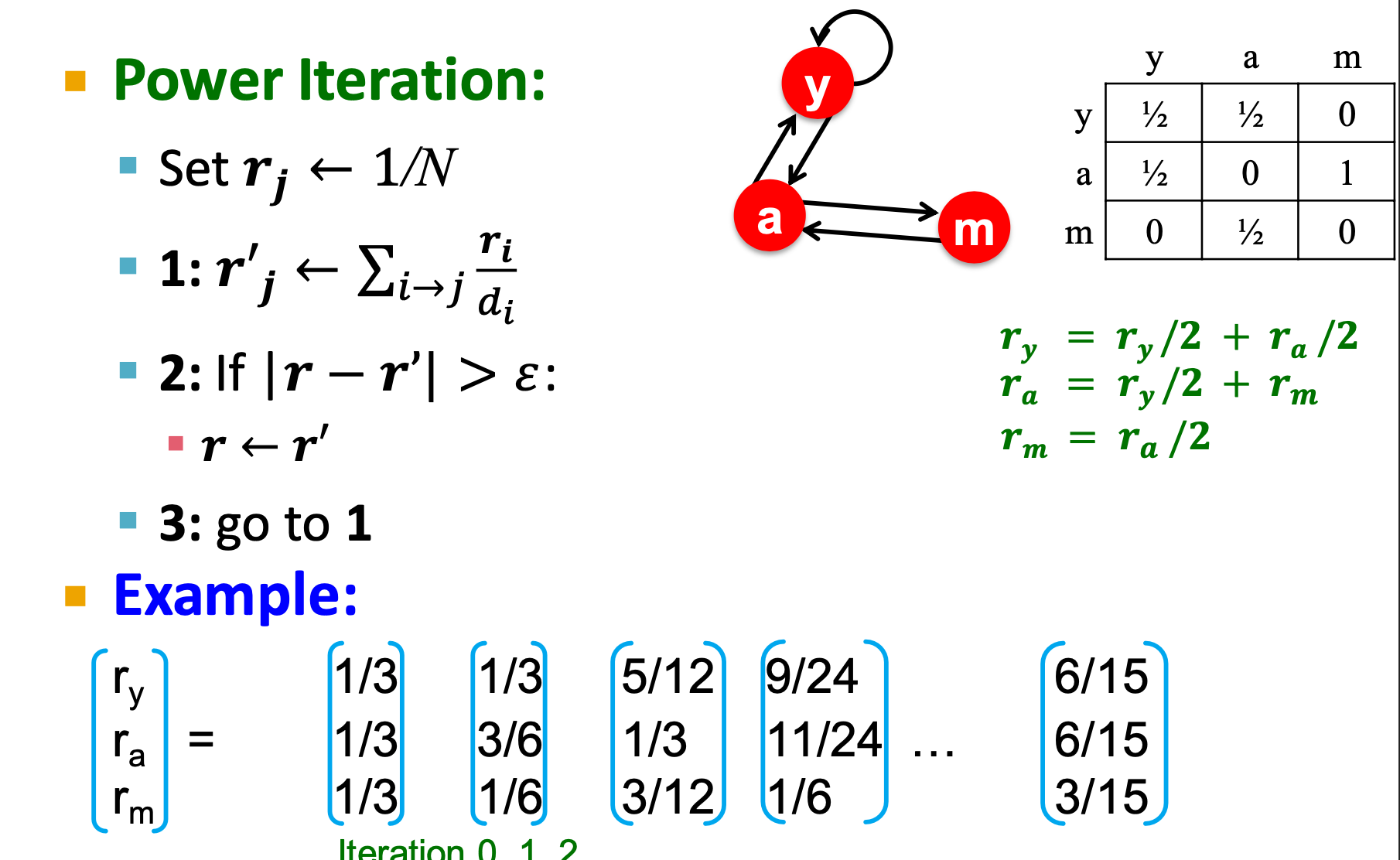
image-20231016144806032

problem

this procedure has 2 problem:

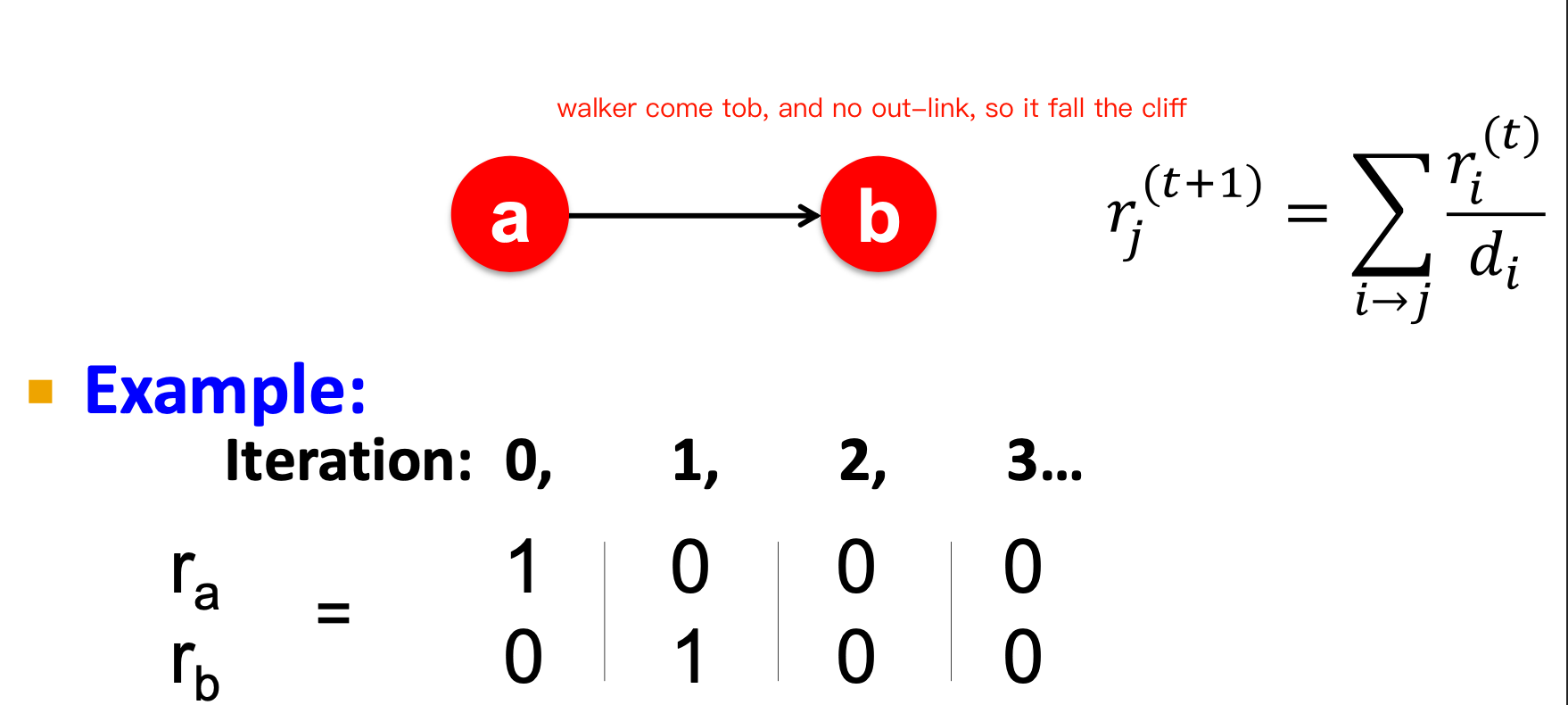
  1. dead ends

    which means the page have no out-links

    it will lead to important ‘fall cliff’

  2. Spider traps

    absorbe all importance

spider trap

image-20231016145129148

Here is solution.

at each step:

  • with the prob. $\beta$, use random link
  • with the prob. $1-\beta$, jump to a teleport
  • Usually us $\beta=0.8\to0.9$

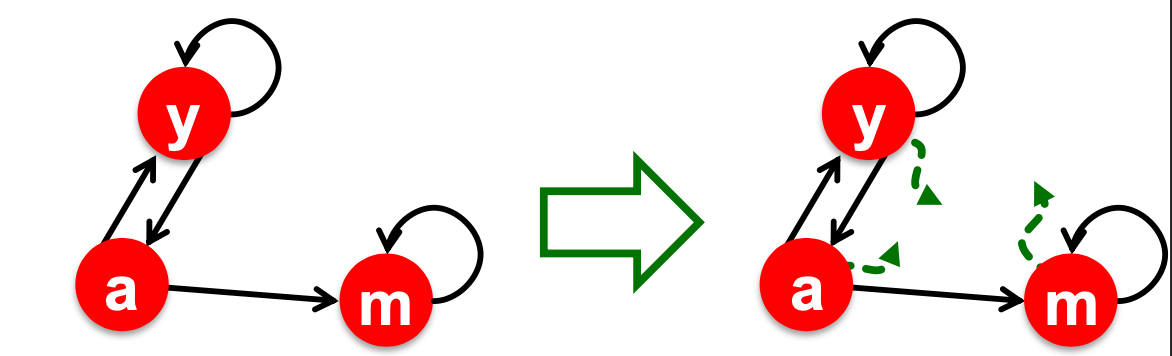
image-20231016145825068

so, use teleport, the surfer will stay at node m, after few step, surfer will jump to the teleport, which could be any node in the graph

dead end

image-20231016145215400

the solution is same with spider trap, just use teleport

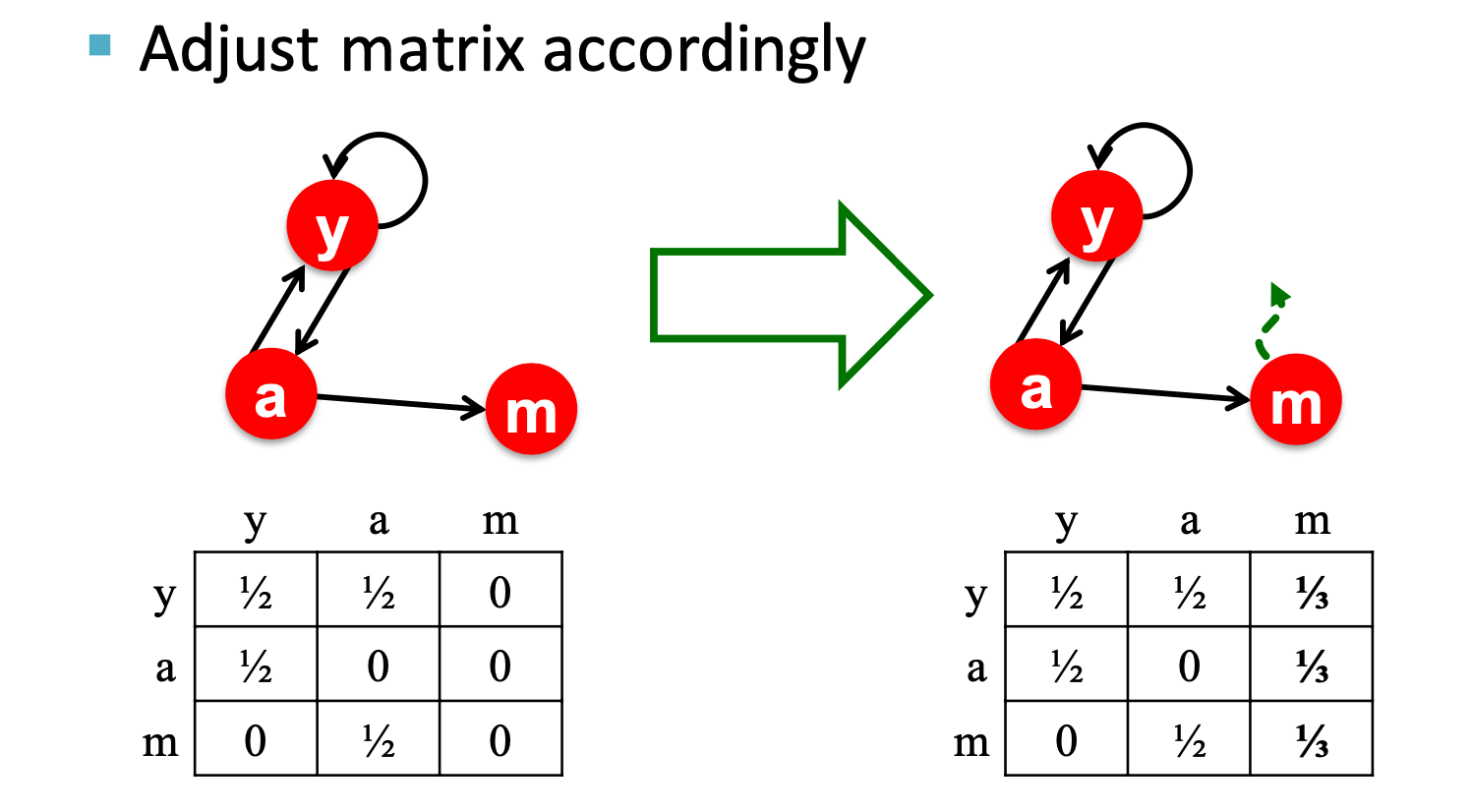
image-20231016150936154

see node m, it has no out-links, we use teleport, and each prob. is $\frac{1}{N}$ N is all graph node, include m itself

Google’s solution

image-20231016151116458

e.g.

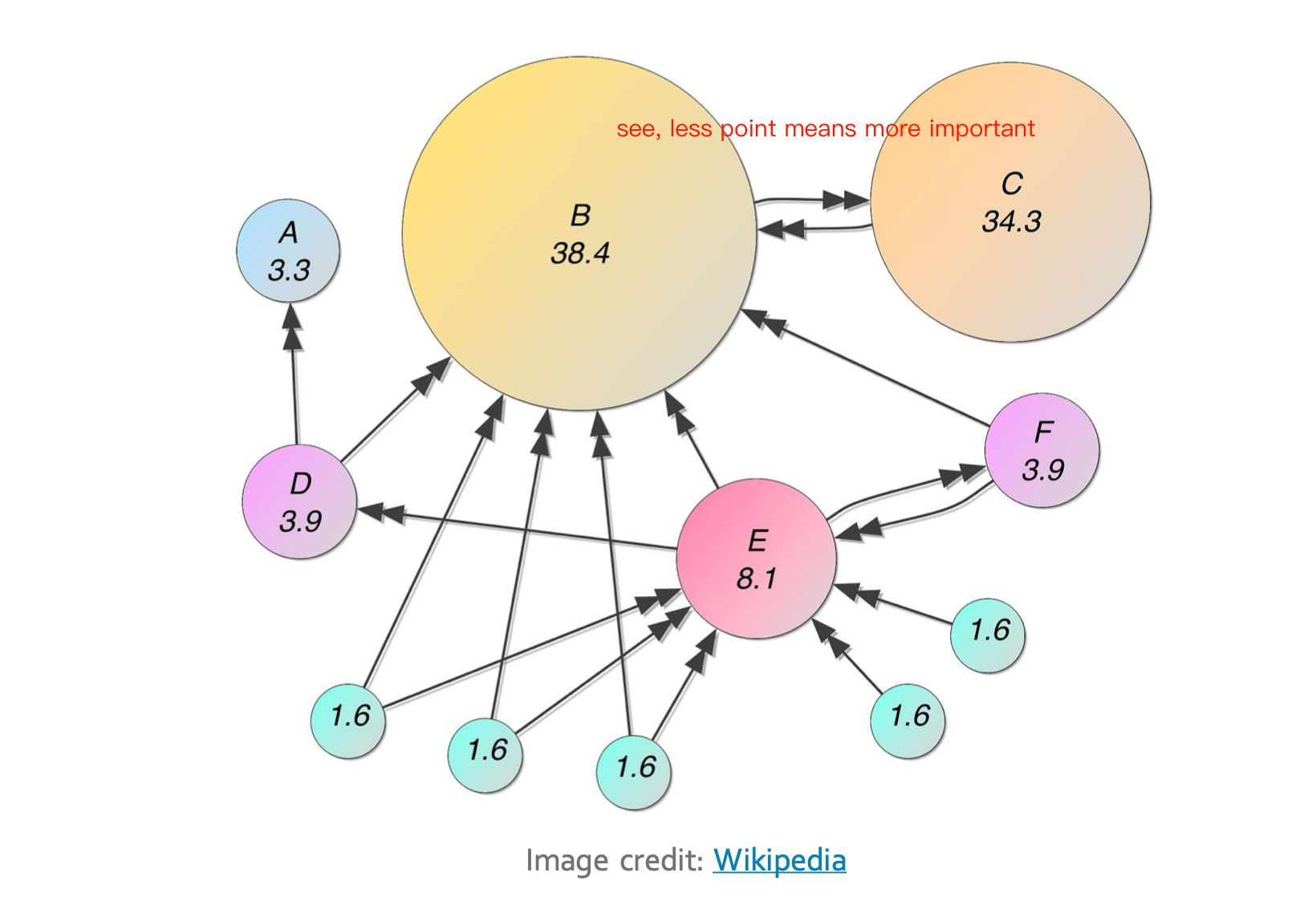
image-20231016151135339

because of teleport, the gree nodes, which have no in degree, also have their importance. and we can adjust $\beta$ to change its value, according to the reality. if it is important than we set, then we set $\beta$ lower.

personalized and restart pagerank

let’s see the difference:

  1. pagerank

    jump to any node

  2. Personalized pagerank

    Jump to a set of teleport nodes $S$

  3. random walks with restart

    teleport to the starting node : $S={Q}$

the form in simulation:

image-20231016155859558