ch2讲的就是我们如何设计特征,来尽量准确的表示这个网络,然后再交给机器学习算法如SVM,最后得到我们的预测:
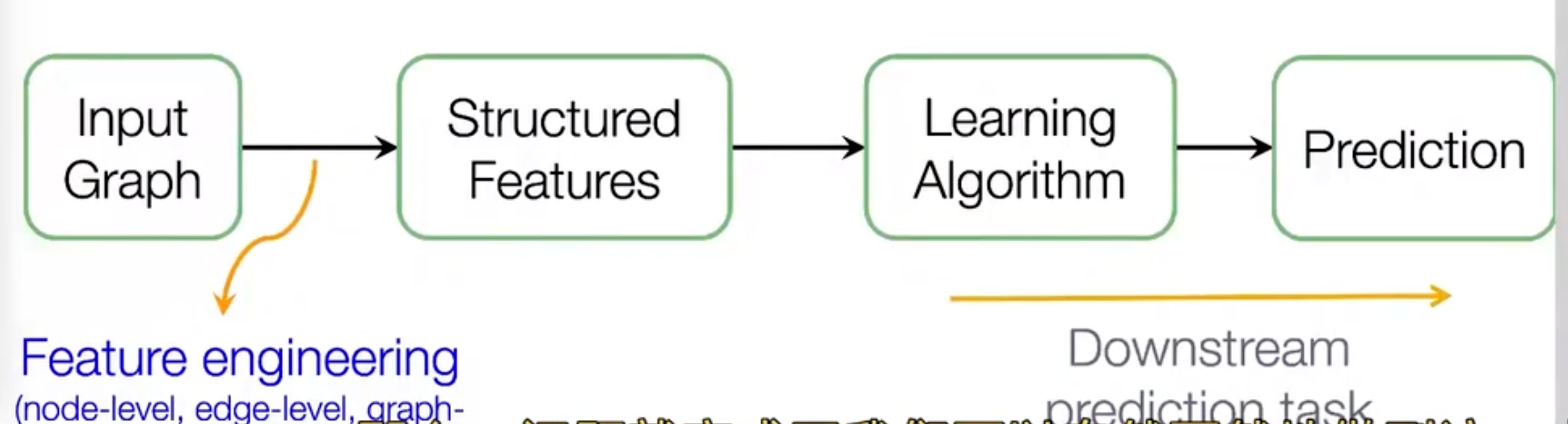
事实上我们可能会花大部分的时间去做特征工程。
这一节考虑的是,能否不用特征工程。
图表征学习:自动获取网络的特征。
node embedding
结点嵌入两个很重要的特征;
- 无监督:训练不需要利用结点的label,也不需要feature
- task independent:嵌入就是一个提取网络特征的过程,可以将提取出的特征用于任何适合的机器学习算法,也就是与下游任务无关。
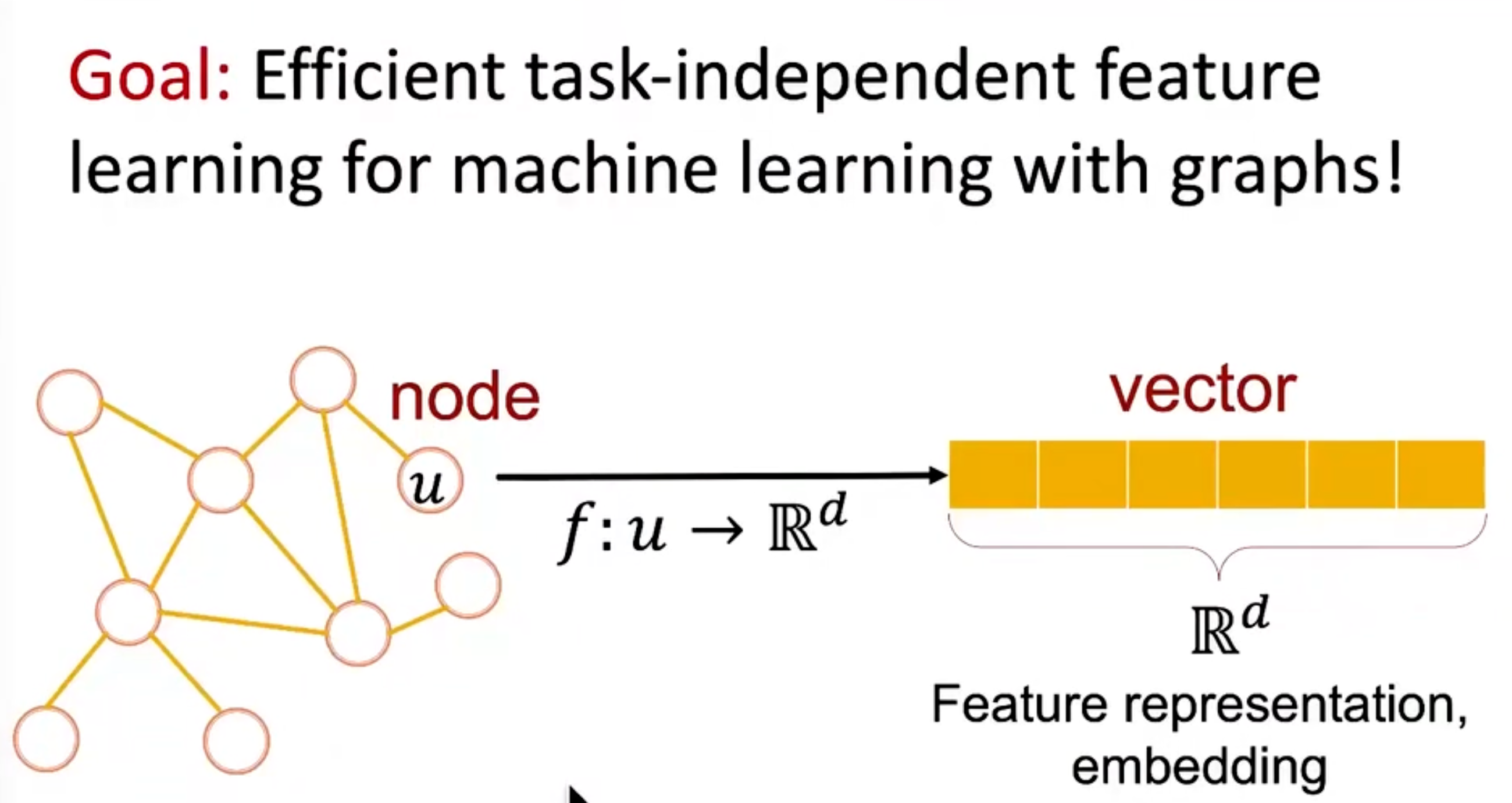
图嵌入是干这样的一件事:将node u自然而然的映射(map)到一个d维的向量中去。这个过程被称为node embedding
嵌入的原理是这样的:如果两个node的d维向量有相似性,那么这两个node本身也很可能有相似性。
完成了结点嵌入之后,我们就可以用这个d维的向量来做downstream task了
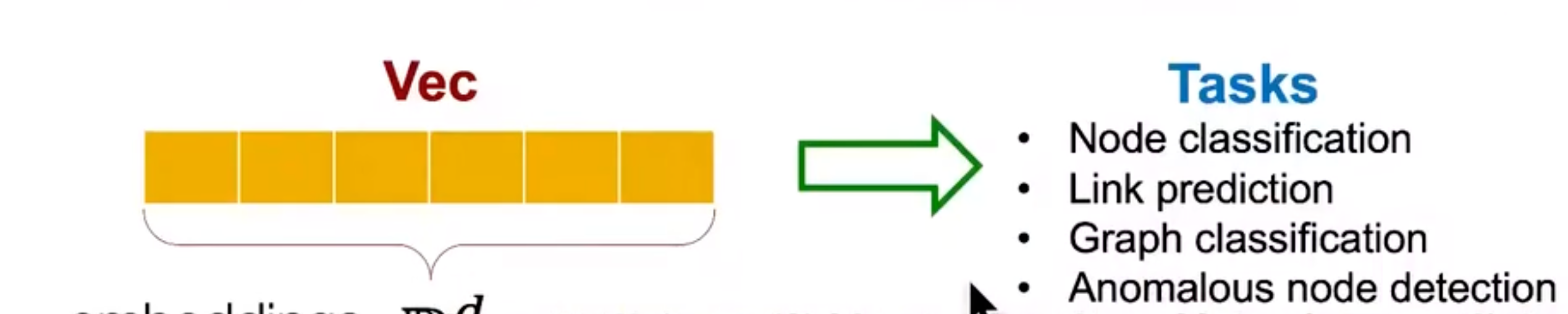
DeepWalking
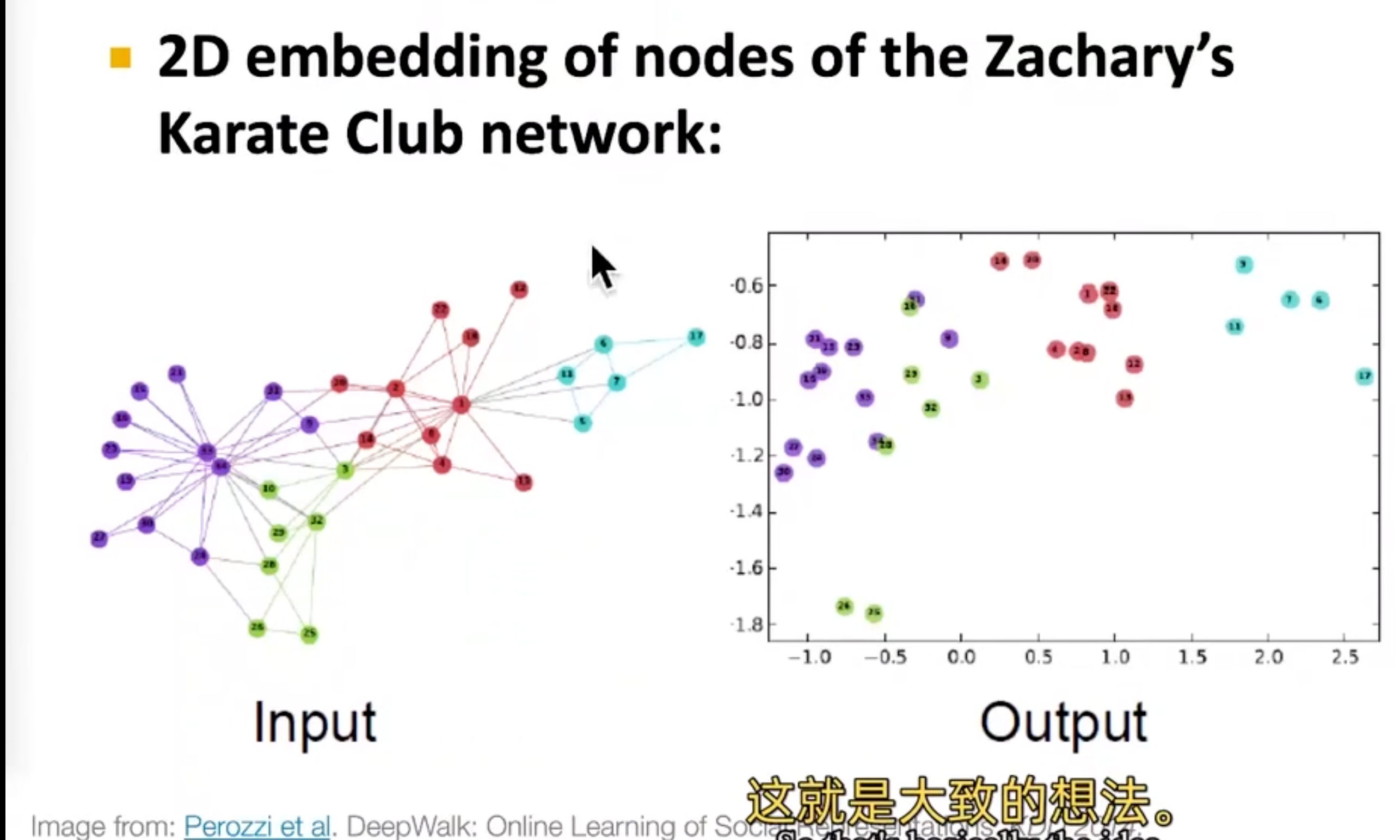
这是一个小型的网络,将图嵌入到了一个2d空间,可以看到相同颜色的结点在图上和被嵌入的空间中都是离得比较近的。
Embedding
更抽象的描述是这样:
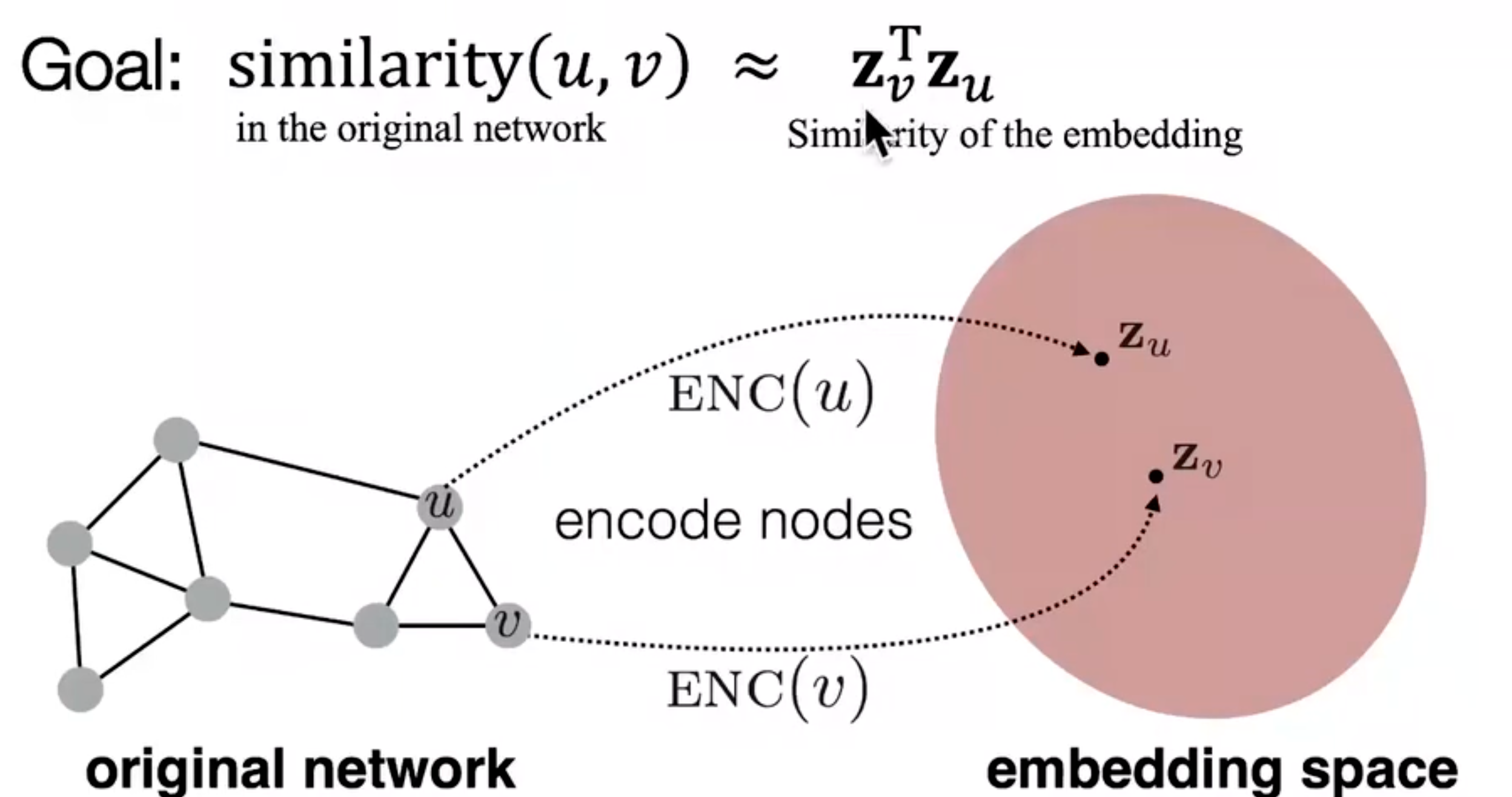
至于用dot product(点积)的原因是,其代表的是这两个向量之间的余弦,例如如果两个向量是垂直的话,dot product就为0了。
嵌入的步骤:
使用Encoder将node映射到嵌入空间
$ENC(v)=z_v$
这个嵌入空间通常是64d到1000d的
定义一个结点相似函数,用来测量图中被嵌入到node pairs之间的相似度
使用Decoder将嵌入结点映射为相似度
优化Encoder的参数,使得结点相似度和嵌入结点相似度近似相等。
$$
similarity(u,v)\approx z_v^Tz_u
$$
这里我们选择的解码器是非常简单的,仅仅是两个向量的dot product
shallow encoder
最简单的编码方式:
$$
ENC(v)=z_v=Z.v
$$
- Z:要学习的矩阵,行代表的是低维向量,列代表的是结点。
- v:v是一个列向量,其中大部分元素是0,除了要得到的结点v的那一个地方为1。
如$v=[0,0,1,0,0,0]$
对于这种编码器,我们需要学习的就是Z:
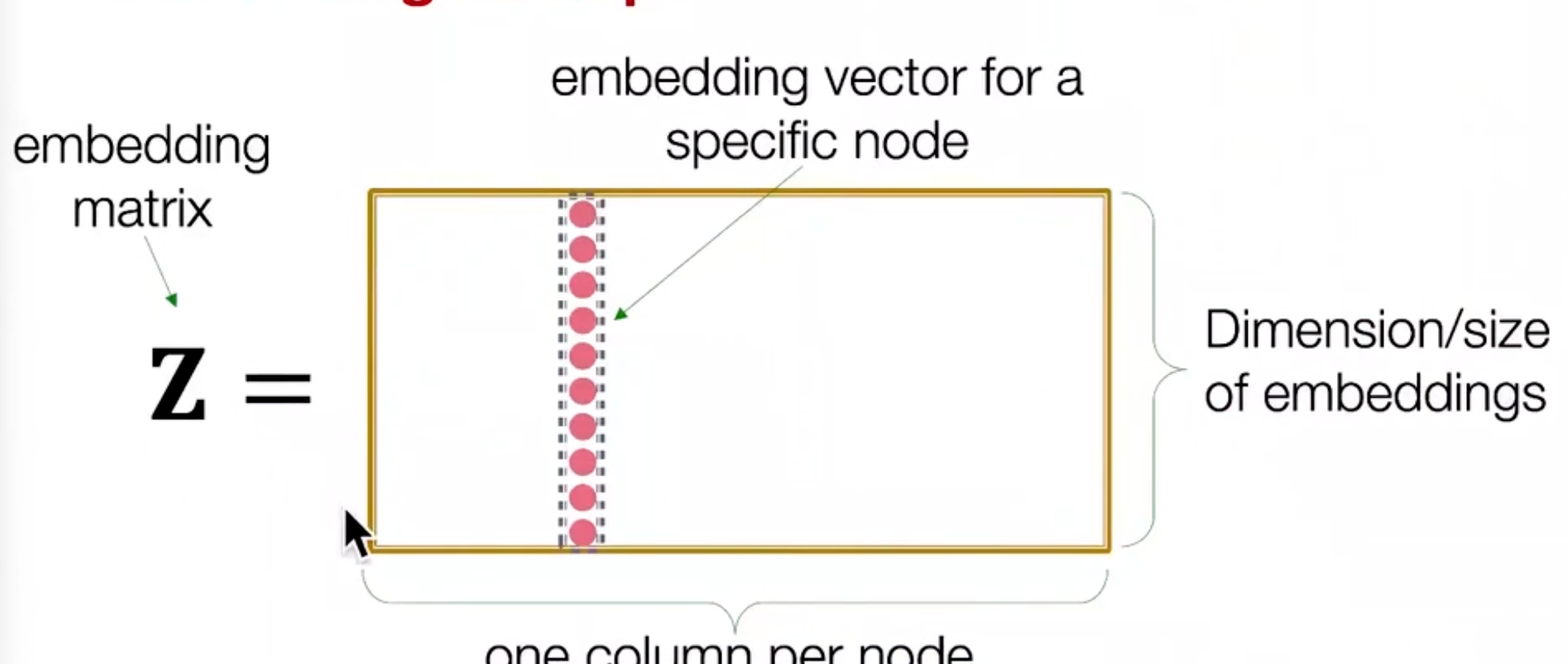
这个方法的缺点:当图比较大时,假设嵌入维度为1000,结点数为100w,那么就有10亿参数。而造成这个matrix如此大的原因是:我们计算了每个node的嵌入向量,当需要某个node的嵌入向量时,可以直接从这个超级大矩阵里面去做一次查找(look-up)。
那么最后,我们来考虑怎么来定义node similarity?可以采用random walks
Random walks
DeepWalk
notion
回顾一下 两个非线性函数:
- softmax
这里给到softmax的解释:a soft version of a maximum function,最大值函数的软版本。
- sigmoid
sigmoid可以任何实数压缩到0~1之间。
另外还有两个概念:
- $z_u$:结点u的嵌入
- $P(v|z_u)$:从u开始,使用随机游走访问v的概率
那么什么是随机游走呢:从一个结点u开始,随机的选取它的一个邻居v,作为next step,依此类推。
这里给了下面这个定义,不是很理解:

detail
基于随机游走的嵌入可以用两步表示:
使用一个策略R,来估计访问结点v的概率
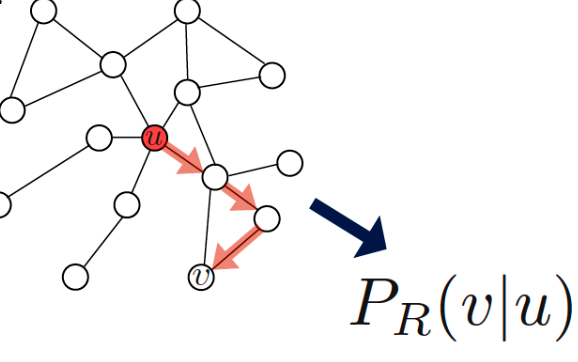
优化嵌入,通过编码这一步随机游走
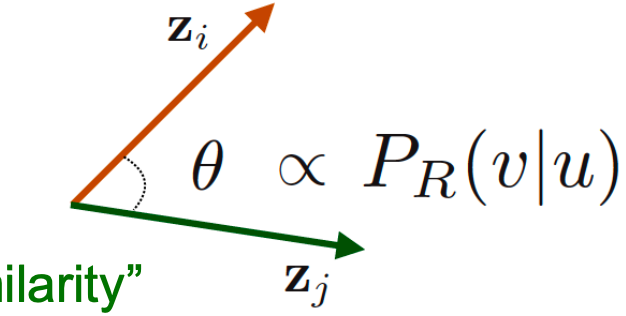
然后为什么选随机游走(优点):
- 如果从u开始,走了v,那么可以认为u和v是类似的
- 不需要考虑整个图全局信息,只需要考虑path中同时出现的random walk
随机游走步骤:
从每一个u开始,走固定的长度,通过使用随机策略R
对于每一个u,收集其$N_R(u)$
通过对数似然函数进行优化:
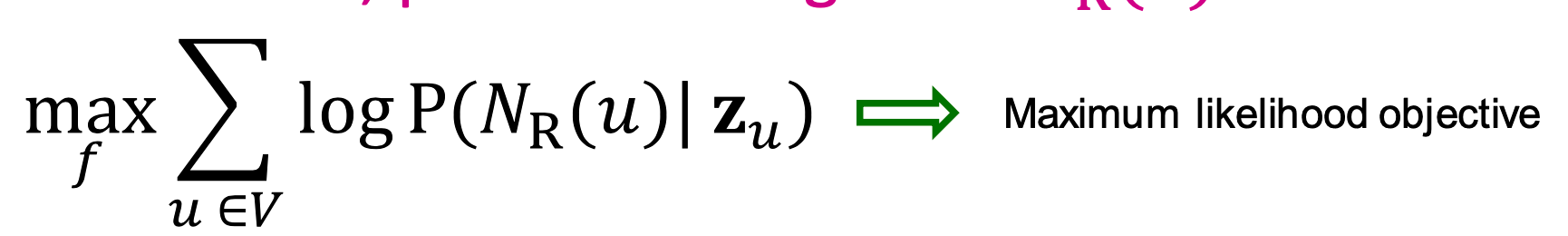
同样也可以讲其表示称下面这种形式:
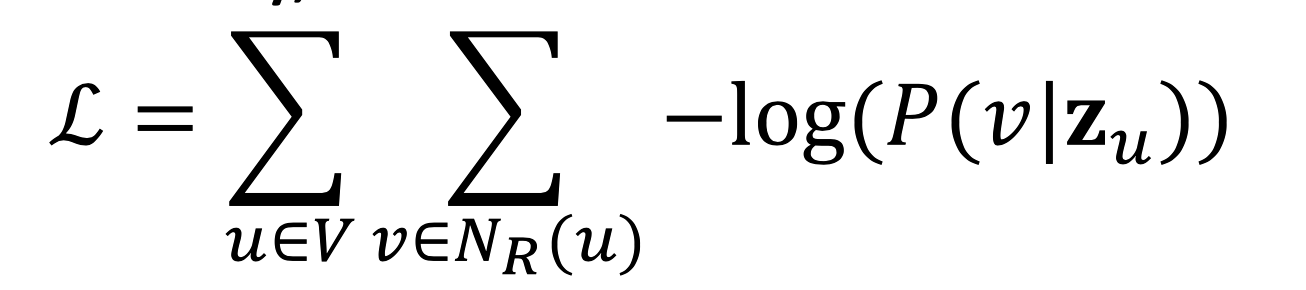
其中可以将对数里面的参数写成下面的softmax形式,那么这个结果其实就是u之后v的概率
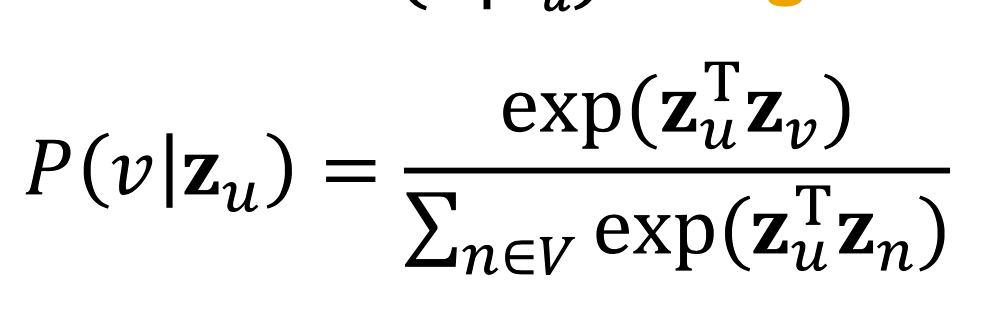
所以最终的损失函数如下:
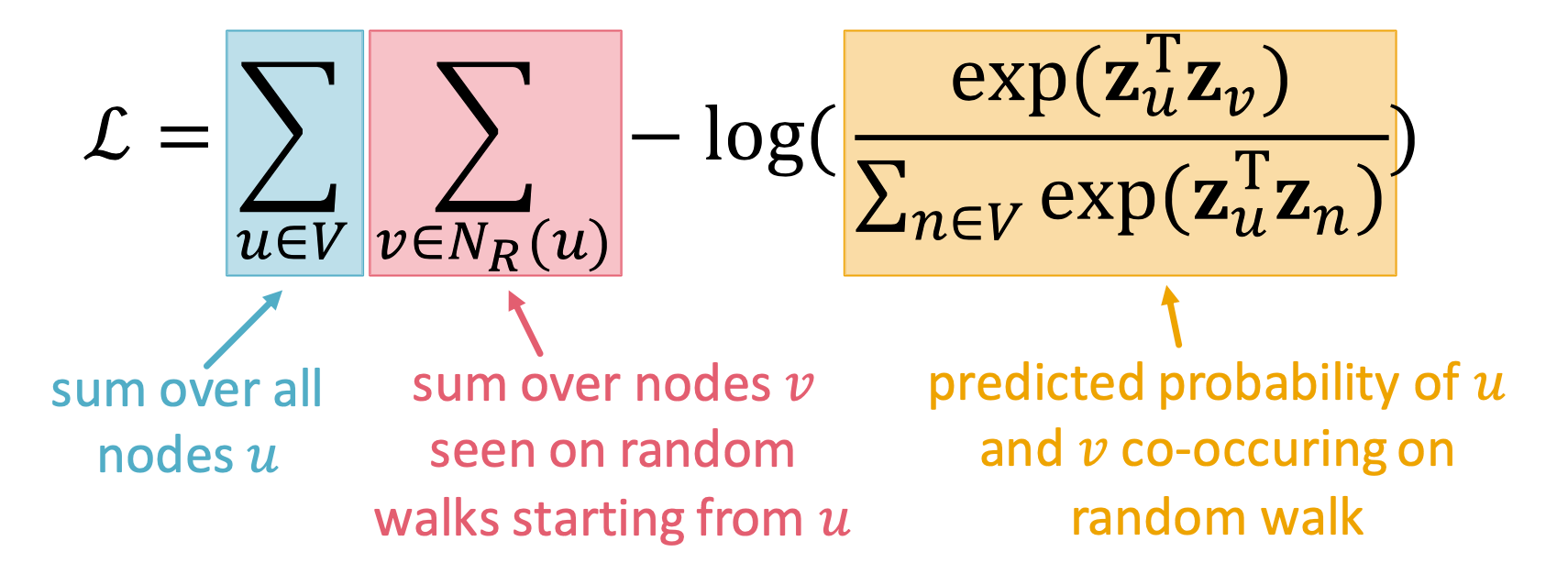
但是有个问题,这里有两层嵌套,意味着时间复杂度是$O(|V|^2)$,复杂度太高了!
negative sample
选择使用负采样来近似softmax的分母:

k是一般取5~20
最开始是DeepWalk提出了random walks(走固定长度,使用随机策略)。这样的similarity表现还不错,从最终结果来看,嵌入空间和图空间中,nearby的点是对应的。

但是这样定义的similarity太受限制了,于是很多人尝试优化。
node2vec
idea:使用灵活的、有偏好的随机游走,例如当进行下一步时,可以选择更广或者更深,也就是DFS和BFS的思想

这里面有两个参数:
- p:可以看到之前的结点
- q:选择使用DFS(outwards)还是BFS(inwards)
下面这例子完美表示了两个参数的用途:
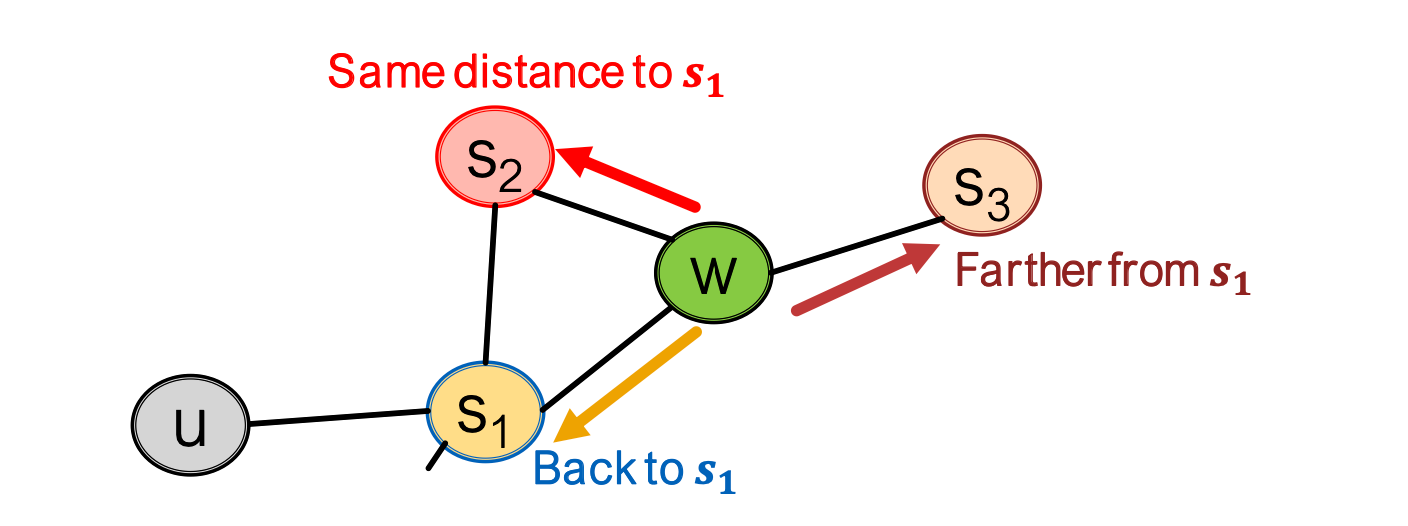
w从s1来的,那么下一步,若是选择inwards,可以去s2(和s1距离相同),若是选outwards,可以走s3,还可以回到s1。
我们将其量化:
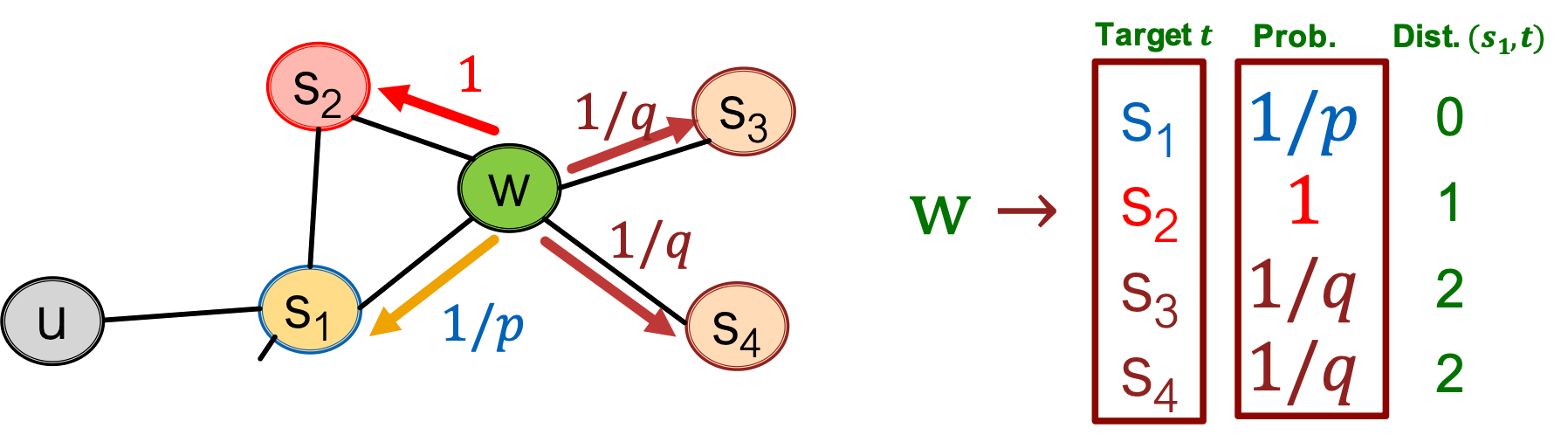
我们可以调整p、q来得到不同的策略R。
other random walk
这是一些其他的关于随机游走的优化。

Embedding entire graph
Goal: to embed the entire graph or sub-graph!
entire graph
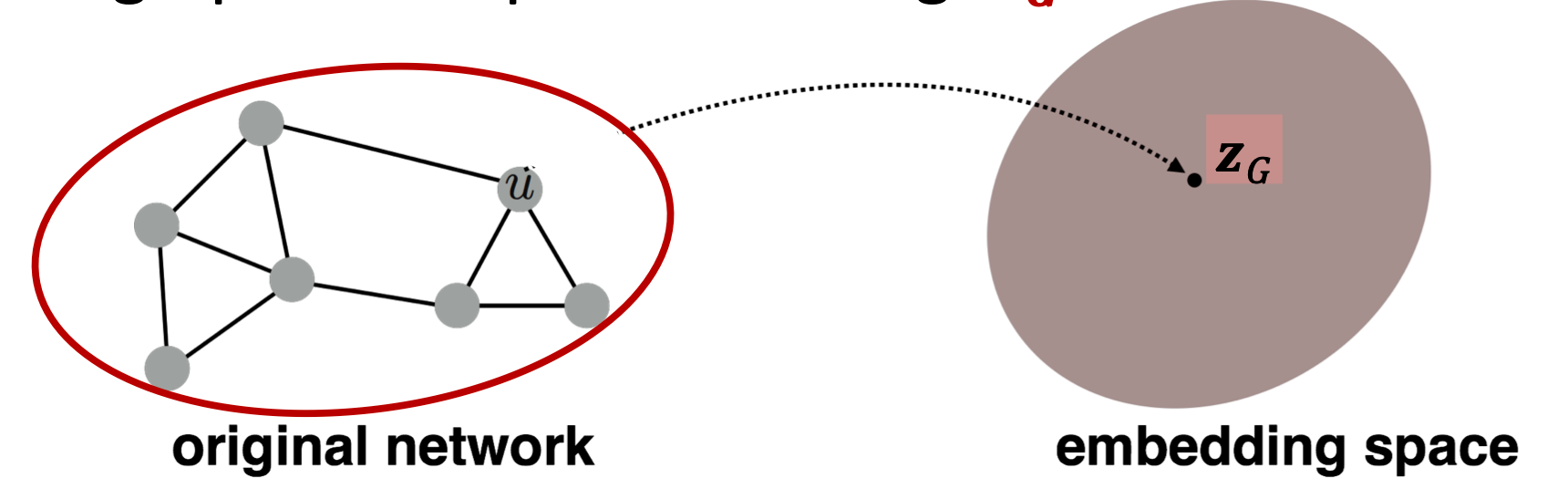
Sub-graph
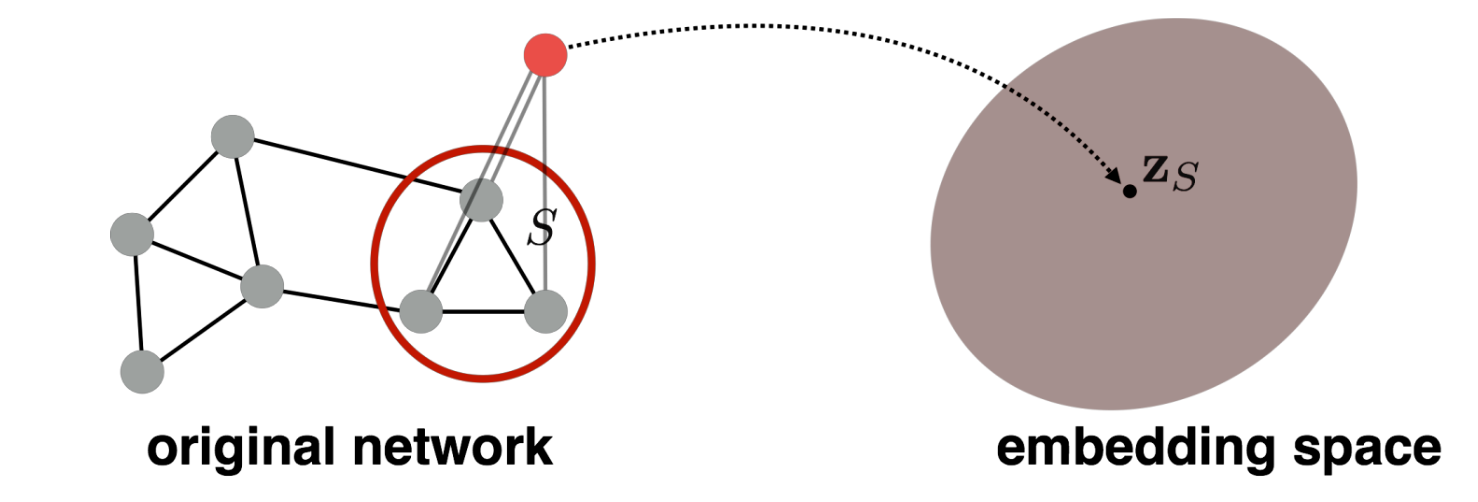
the application(task):
- Classifying toxic vs. non-toxic molecules
- Identifying anomalous graphs
Approach 1
it is simple and effective, which is:
use node2vec or deepwalks to caculate the embed node u of $z_u$
then sum or average
$$
z_G=\sum_{v\epsilon G}z_v
$$
Approach 2
use a virtual node to represent the graph, and by using node2vec or deepwaks to embedding the virtual node to embedding space.
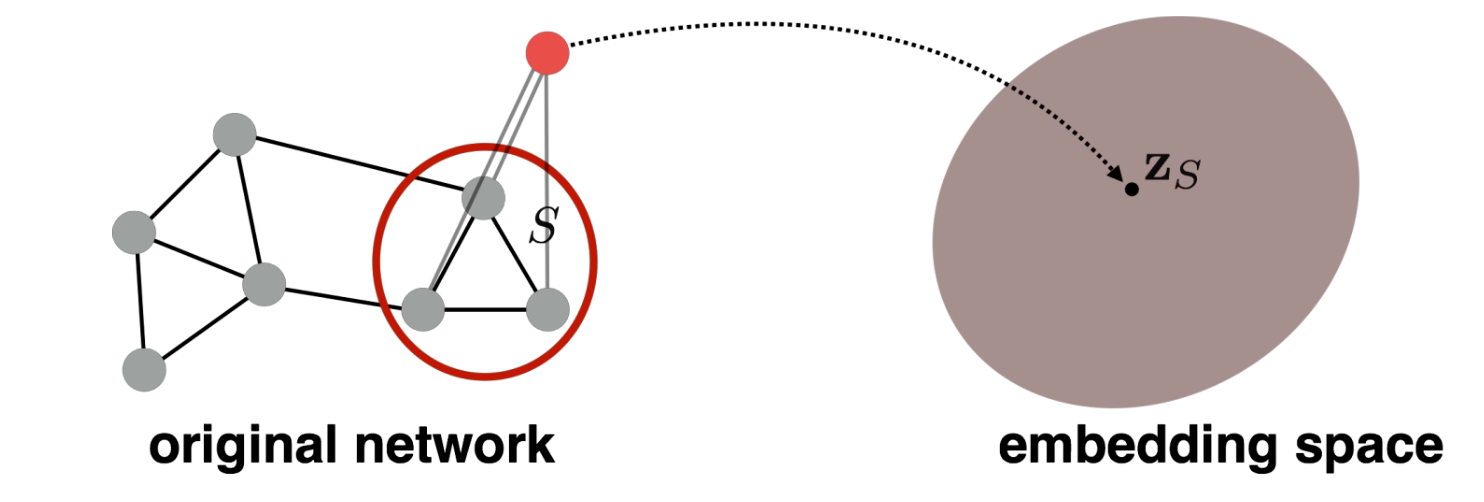
Approach 3
Idea 1
use anonymous walks to instead random walks.
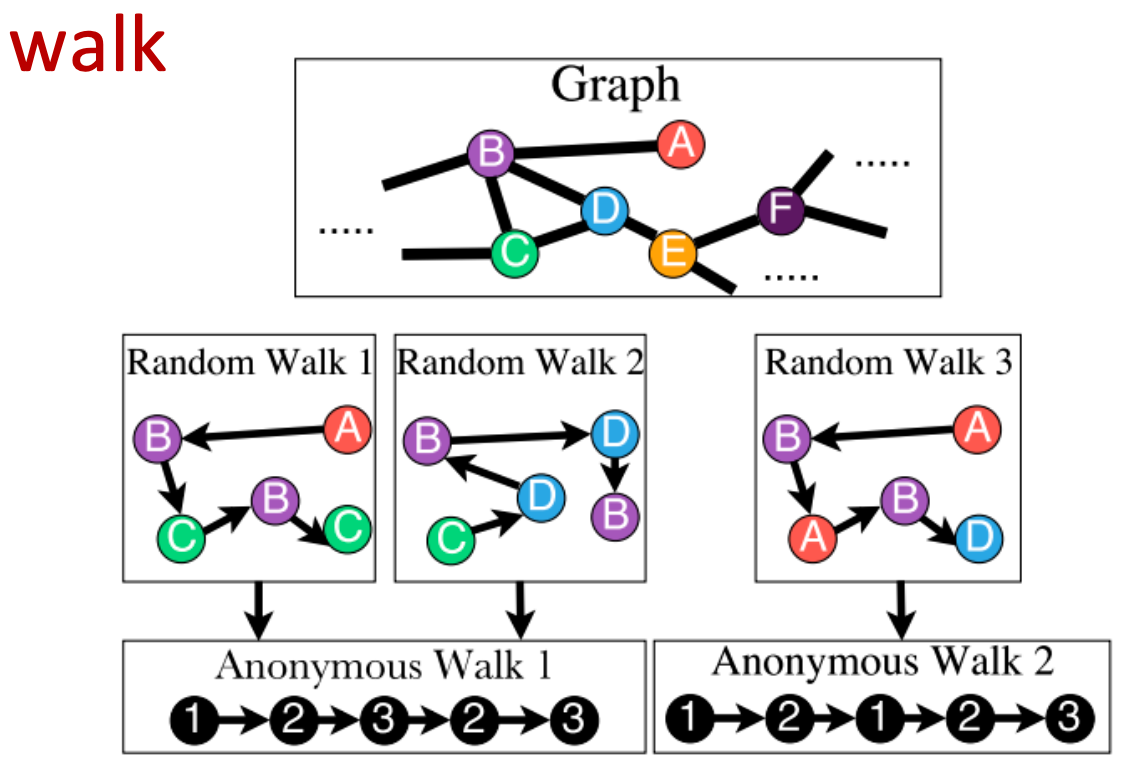
feature is:
- Anonymous
- Capture the struct rather than node pairs
with the length of step increasing, the number of anonymous walks (the anonymous walks vector $Z_G(i)$, for l=3, the dimensions of $Z_G(i)$ is 5) exponentially increase.
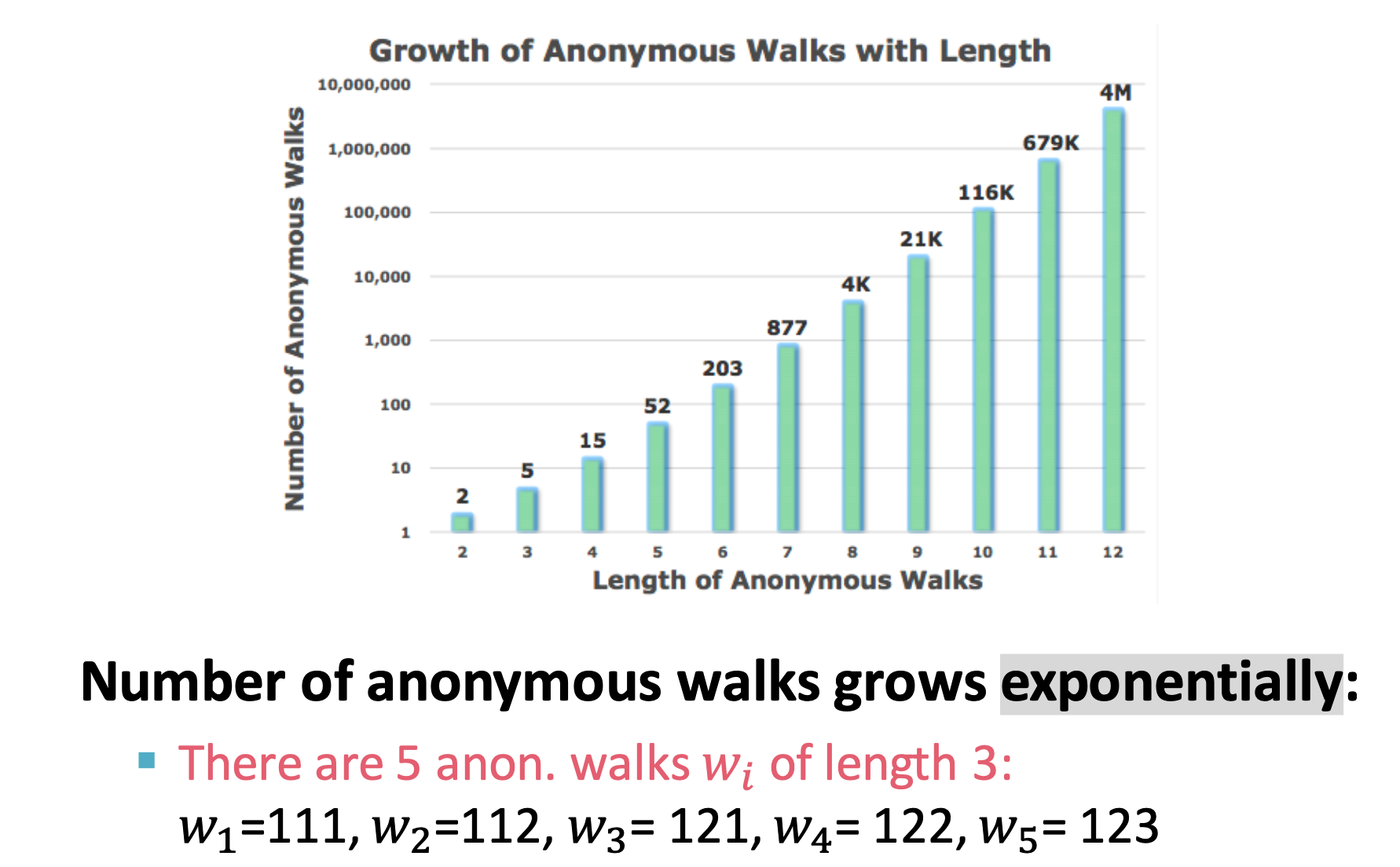

We have the vector now, so how many walks should we sample to represent the whole distribution?
use this formula:

Idea 2
Above, we use a vector $Z_G(i)$ to represent the distribution, it is a set of probability about every walk.
the other idea is use walks ranther than probability:
$$
Z={z_i:i=1…\eta} \
$$
$\eta$ is the number of sampled anonymous walks.
so here is the idea and how we learning the walks embeddings?
First, sample some walks:
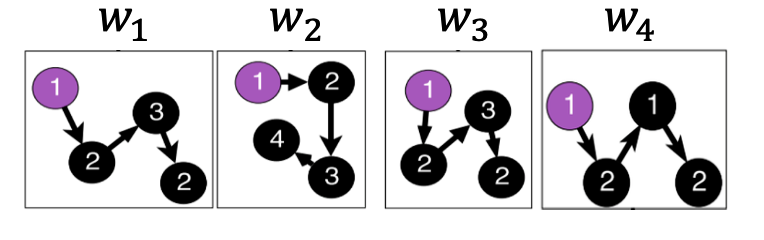
Than, learn to predict walks which is co-occur in $\Delta$ size window
e.g., predict $w_3$ given $w_1,w_2,\Delta=2$
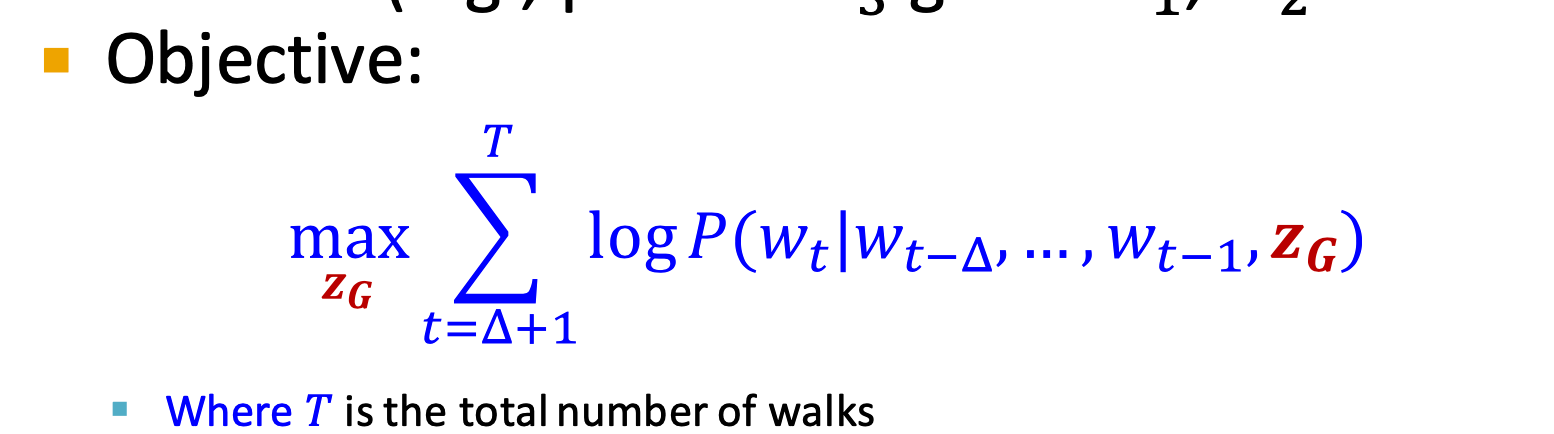
so, different from DeepWalk, node2vec, the neighbor set is:
$$
N_R(u)={w_1^u,w_2^u…w_T^u}
$$
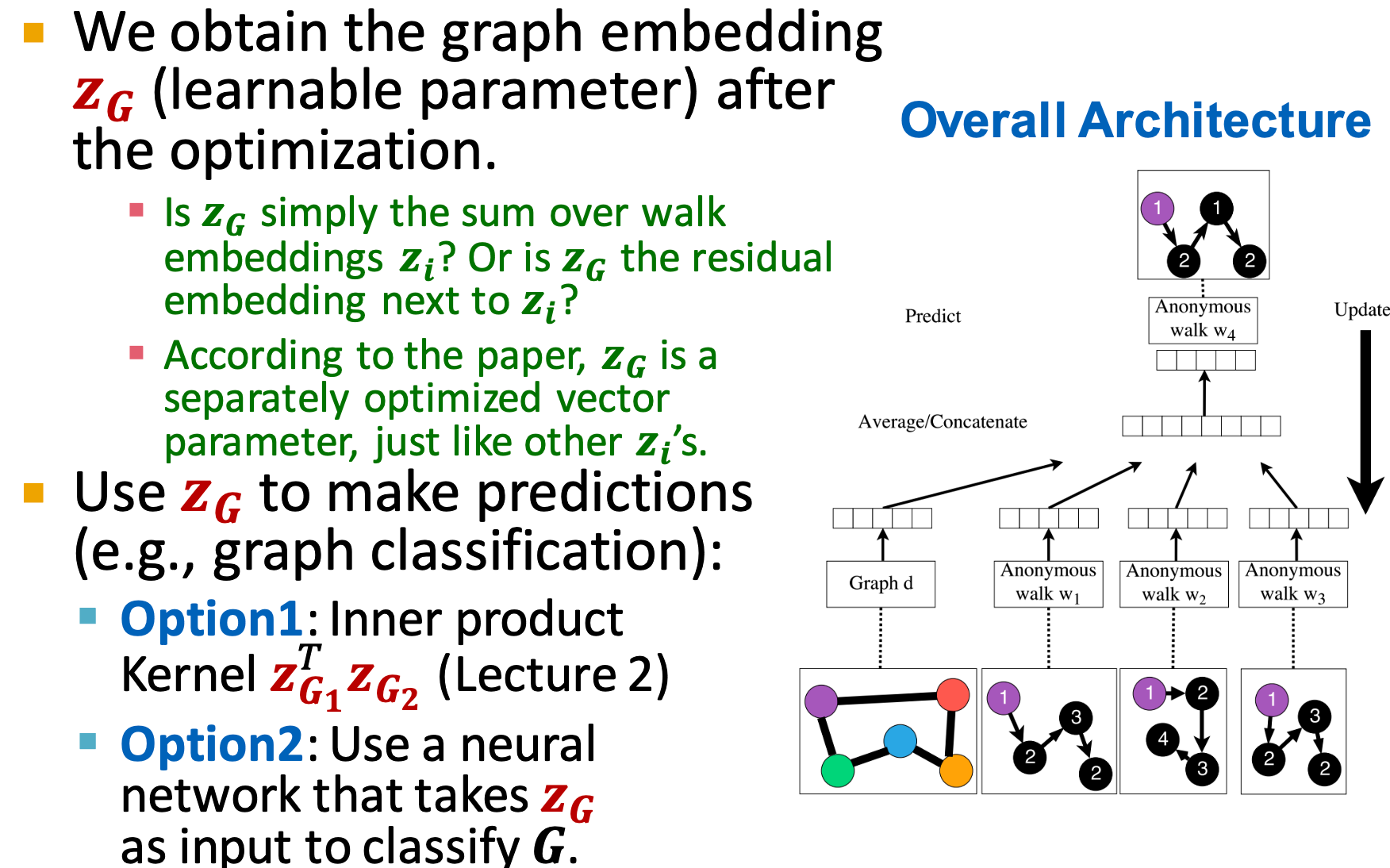
$Z_G$ is a optimized vector parameter