信号的基本概念
信号的定义：随时间变化的有限实值函数。其有两个特性：
- 实值性：信号的取值都是实数。
- 有限性：信号的值是有限值，从功率的角度来看，功率是有限的，能量是有限的，信号自然也是有限的。
以确定性为标准，信号可分为确定信号和随机信号：
- 确定信号：对于任意时刻，都可以确定信号的值。
- 随机信号：只能从概率分布的角度描述随机信号的相位or幅度。
从时间变量（定义域）的取值是否连续可分为：连续信号 or 离散信号
从定义域以及值域的取值是否连续（同时，二者都），可分为模拟信号 or 数字信号。
信号的时域描述
对模拟信号$x_a(t)$从时间上进行采样，可得到离散信号$x(n)$:
$$
x_a(t)|_{t=nT_s}=x_a(nT_s)=x(n)
$$
公式(1)展示了采样的原理。其中$T_s$表示采样周期，采样频率$f_s=\frac{1}{T_s}$
例如，对于离散正弦信号，就可以通过采样模拟正弦信号$x_a(t)=A\sin(2\pi ft+\phi)$来得到：
$$
x_a(t)|_{t=nT_s}=A\sin(2\pi fnT_s+\phi)=A\sin(\Omega T_sn+\phi)=A\sin(\omega n+\phi)
$$
其中，$\omega$为数字角频率，$\Omega$为模拟角频率。
复信号（欧拉公式）：
$$
e^{j\omega n}=\cos(\omega n)+j\sin(\omega n)
$$
信号的频域描述
离散傅立叶变换DTFT：
$$
X(e^{j\omega})=DTFT[x(n)]=\sum_{n=-\infty}^{\infty}x(n)e^{-j\omega n}
$$
由于正弦信号的周期性，可以得到任意信号的DTFT都具备周期性，周期为2$\pi$
时域采样等于频域周期延拓：
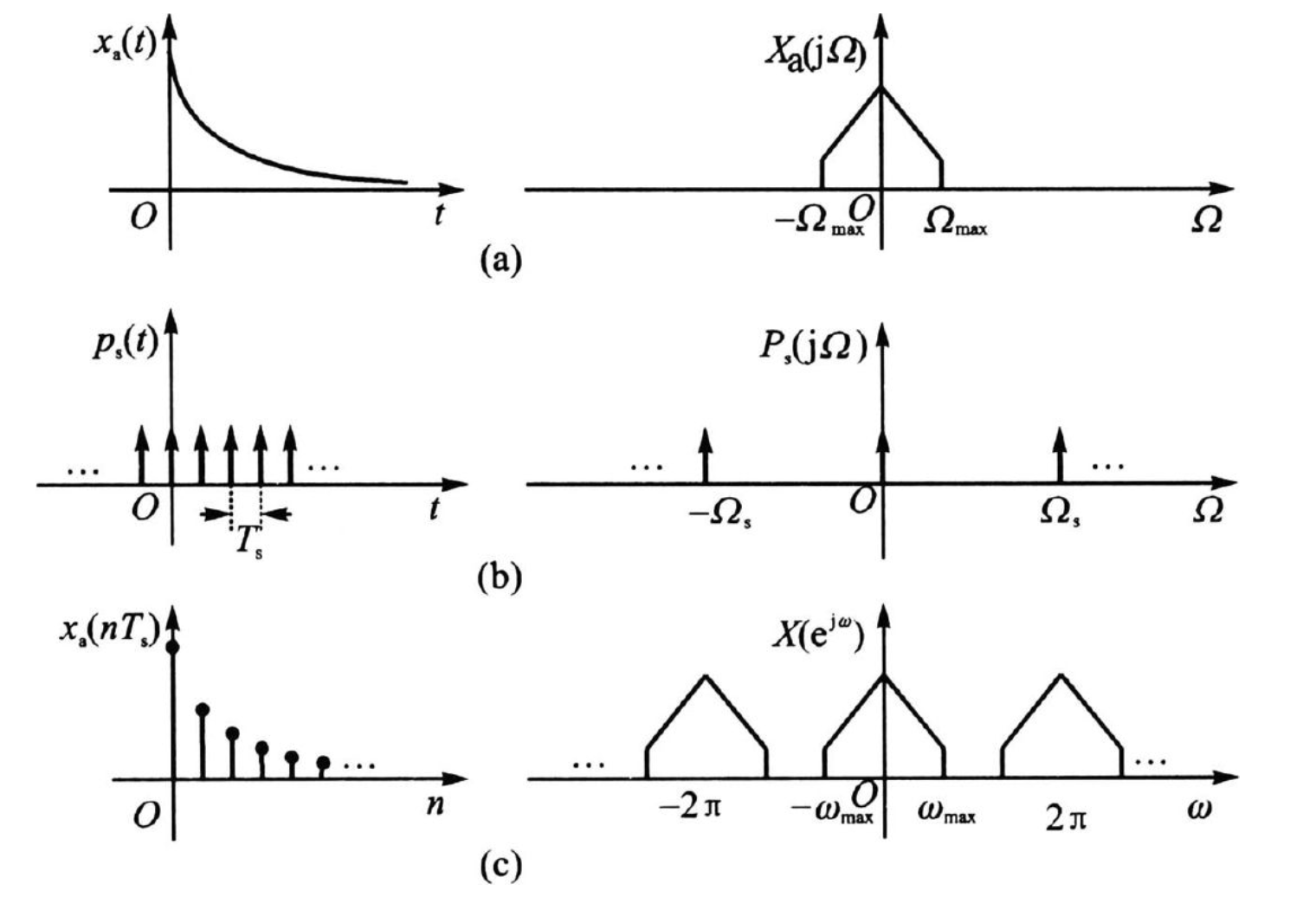
由上图也可得知，要想采样之后能够完全恢复出模拟信号来，要满足下式：
$$
\Omega s<2\pi \
f_s>2f{max}
$$
从模拟信号到数字信号
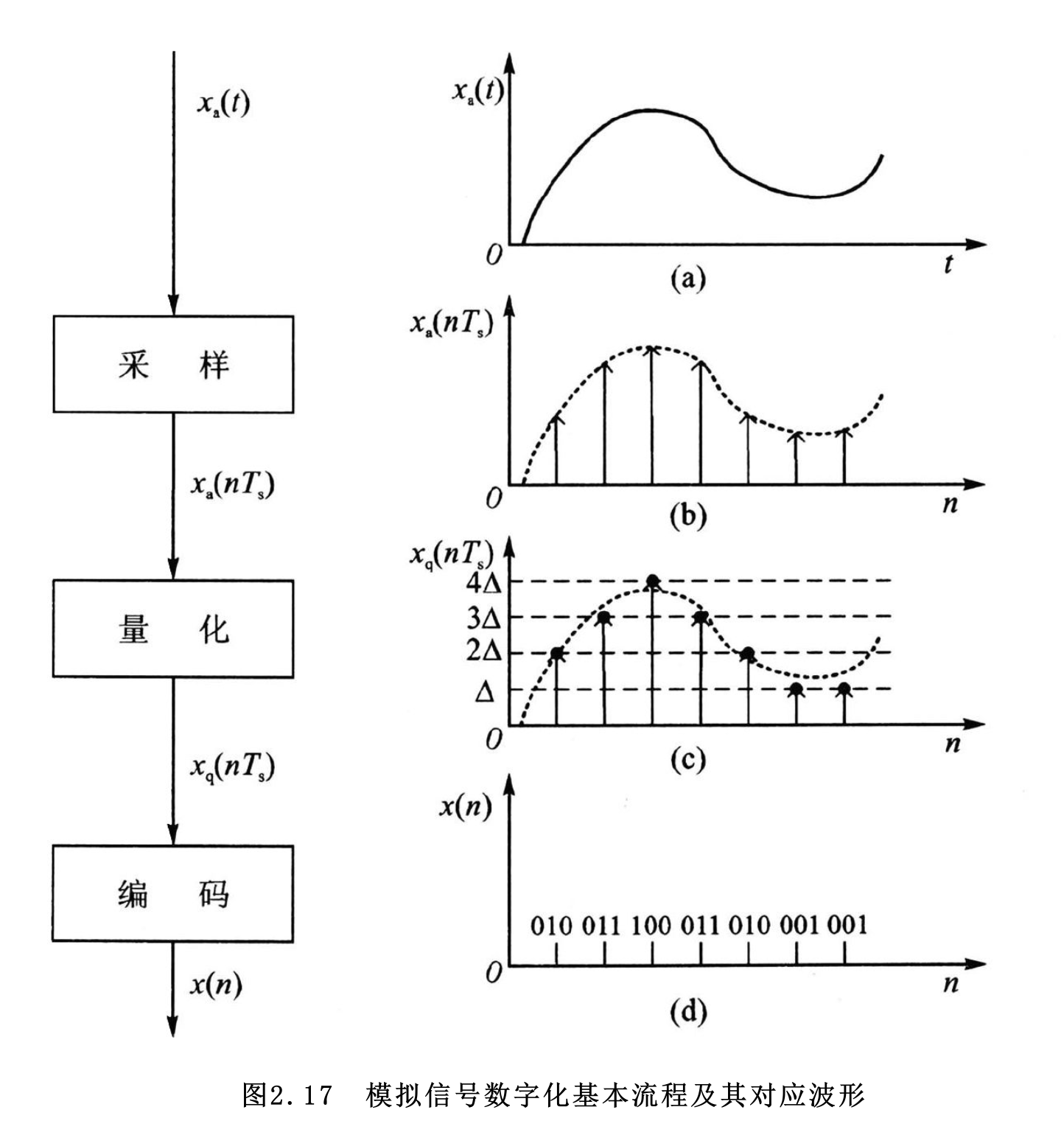
采样
将模拟信号从时间上等间隔采样，得到的是离散时间信号
量化
将每个采样点的幅度以最小化的数量单位$\Delta$的整数倍来度量，这样幅度也是离散的了，得到的是数字信号
编码
对幅度进行二进制编码
参数选择
前面讲了满足采样定理之后，可以保证采样之后的信号频谱不发生混叠。但是现实中可能会有噪声以及其他干扰信号。那么应该如何处理？
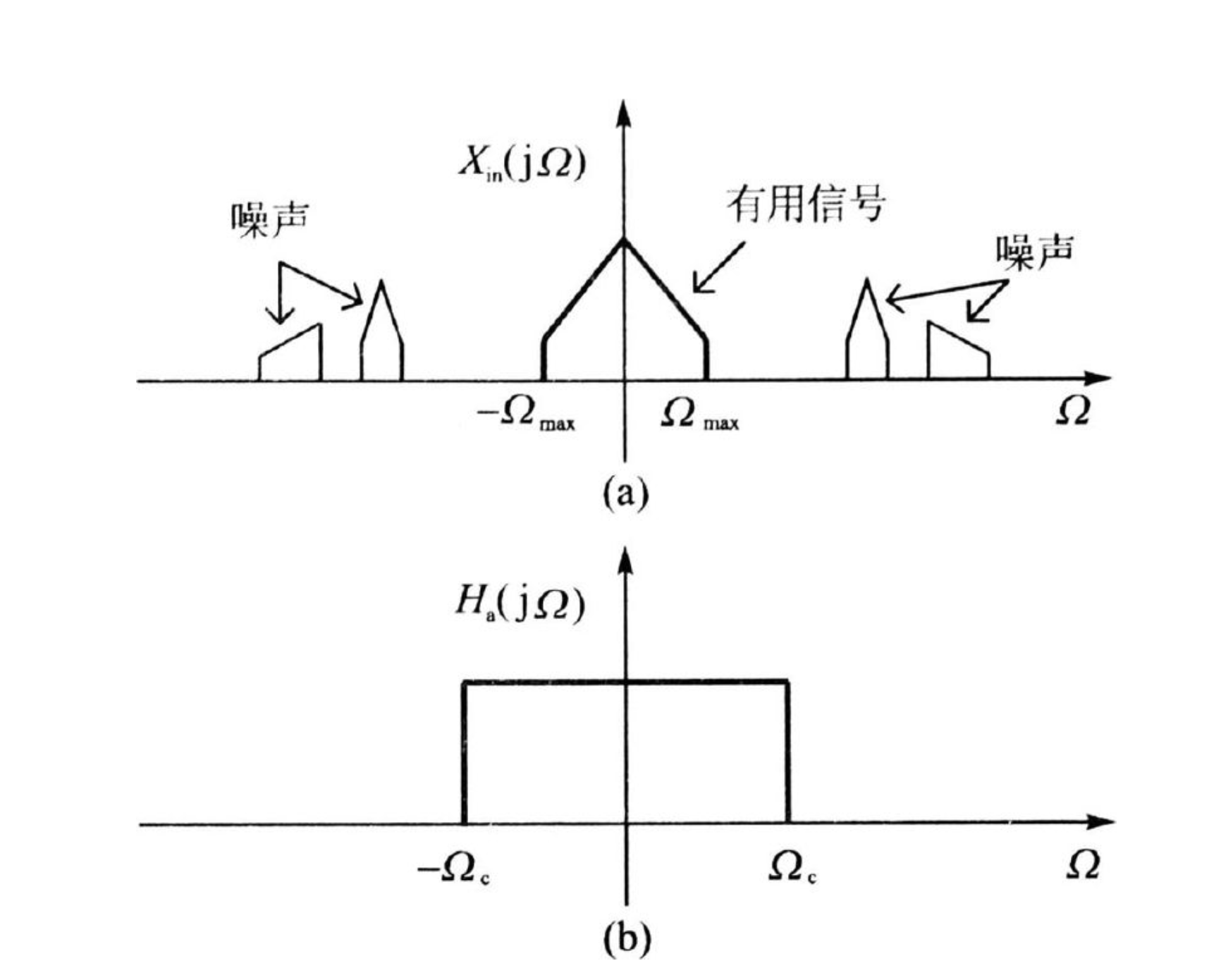title:
加个滤波器做卷积即可
