d2l

d2l

经典QA

问题1.怎么根据输入空间，选择最优的深度或者宽度

假设问题背景：128 input，2 output

  1. 首先尝试线性回归模型，128输入2输出，不要隐藏层。
  2. 然后试试mlp（多层感知机）：128 input -> 128/64/32/16/8 hide -> 2 output。然后在此基础上挑出比较好的隐藏层个数，比如128和8不行，然后64/32/16效果都还不错。
  3. 再试试加一个隐藏层，比如128 -> 64 -> 16 -> 2，或者: 128 -> 32 -> 8 -> 2。多跑几轮。

多调几次就有经验了。

问题2.k折交叉验证的目的是确定超参数吗？然后还要用这个超参数再训练一遍全数数据吗？

有三种做法：

  • 先在train set上训练，然后再用valid set上进行k折交叉验证，来选去hyper parameter，最后再在train set上训练w和b。
  • 在train set上训练后，使用valid set进行k折验证，然后直接选hyper parameter，不训练了，直接作测试。
  • 最贵的一种做法：在k折验证后，得到k个模型，在测试一个样本的时候，k个模型每个模型都跑一遍结果，最后进行平均/投票。

PS：测试集我们可能拿不到label。

问题3.老师说的神经网络是一种语言，意思是利用神经网络去对万事万物建模吧？就是指的它理论上能拟合所有函数？

理论上来讲，只有一个隐藏层的、神经元足够多的mlp，就能够拟合所有的函数。但是，训练不出来，因此有了下面几种（原话：我知道mlp能拟合你，但是mlp训练不出来，所以我要做一个好的结构，来帮助你训练）：

  • cnn：假设数据是有空间信息的
  • rnn：假设数据是有时序信息的
  • …

我们引入先验，增加偏好，因此有了新的模型，试图帮出mlp去训练。

很多时候，我们都是先有一个想法/理由，然后就去做了，很多优秀的论文也是这样，刚开始有个想法，但大部分都是错的，只不过满满的做最后的效果还不错。

三种元素：

  • 艺术：无法解释，就是比较好
  • 工程：能有一套详细的流程
  • 科学：能够解释

神经网络，我们希望他是科学，但做起来是工程，实际上其中百分之五十都是艺术。可能

可能若干年后有人能科学的解释dl，但是，蒸汽机发明之后，100年后才出现了热力学。

问题4.如果训练是不平衡的，是否要先考虑测试集是否也是不平衡的，再去决定是否使用一个平衡的验证集？

周志华老师讲过，可以通过加权来使得正类负类平衡，比如银行卡贷款，10000人中，5个人没有还款。

在李沐老师这里听到了新的做法：

  • 如果采样的数据是独立同分布的，也就是说，现实世界中就是这样分布的，那么其实就直接训练就行了，做好90%的正类，另外10%的负类尽量做好
  • 如果采样不是独立同分布，那么就需要加权了。

这里其实也引入了人为的偏好，采样数据在真实世界中究竟是如何分布，这个很难去界定。

问题5.老师，为什么对16位浮点影响严重？32位或者64位就好了吗？那就是说所有通过fp16加速或者减小模型的方法都存在容易梯度爆炸或者消失的风险？

芯片大小一般是固定的，但是一个64位的浮点单元的面积是16位浮点单元的面积的4倍，因此16位浮点运算的速度也比64位浮点运算的速度快4倍。

另一方面，16位浮点更容易发生上溢或者下溢，所以加速/减小模型更容易出现梯度消失或者爆炸。

问题6.这几个超参数得影响重要程度排序是怎样得，核大小，填充，步幅

卷积神经网络中有kernel_size、填充、步幅三个超参数，首先给出结论：核大小最重要

整个CNN就是在训练核大小，所以这个是最重要的。

然后就是步幅和填充了。

  • 填充主要是为了让我们的输入和输出的形状保持一致
  • 而步幅一般选1或者2，再往上就取决于模型的复杂度了。当步幅为1时，每次我们的输出会比输入小一个维度，也就是说是线性的；而当将我们的步幅调成2，相当于一次就把我们的输入砍了一半，也就是说是指数下降的。当我们的输入太大时，在某几层增大步幅合一使得我们的输出直接少一个量级。

比如，在CNN中我们要做100层的网络，然后我们通过计算要除几次，最后就可以把这几个折半砍的层均匀的插在中间；其余的层都是通过填充使得输入和输出是一样的维度。

环境

安装环境

pip清华源：

1
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple

使用ubuntu22.04后，添加源后，可以通过apt来安装具体版本的python了：

1
2
3
4
sudo add-apt-repository ppa:deadsnakes/ppa
sudo apt-get update
sudo apt install python3.8
sudo apt install python3.8-distutils

安装好后，可以通过下面的指令来找到安装后的位置：

1
which python3.8

然后由于aarch64使用conda有问题，所以就换了一种虚拟环境方案，使用的是：virtualenv+virtualenvwrapper。

操作就三个

1
2
3
4
5
6
7
8
9
10
11
12
chengyiqiu@chengyiqiu:~/Envs$ which python3.8
/usr/bin/python3.8
chengyiqiu@chengyiqiu:~/Envs$ virtualenv -p /usr/bin/python3.8 d2l
created virtual environment CPython3.8.17.final.0-64 in 1184ms
  creator CPython3Posix(dest=/home/chengyiqiu/Envs/d2l, clear=False, no_vcs_ignore=False, global=False)
  seeder FromAppData(download=False, pip=bundle, setuptools=bundle, wheel=bundle, via=copy, app_data_dir=/home/chengyiqiu/.local/share/virtualenv)
    added seed packages: pip==23.2.1, setuptools==68.0.0, wheel==0.41.0
  activators BashActivator,CShellActivator,FishActivator,NushellActivator,PowerShellActivator,PythonActivator
chengyiqiu@chengyiqiu:~/Envs$ ls
d2l  py38
chengyiqiu@chengyiqiu:~/Envs$ source ./d2l/bin/activate
(d2l) chengyiqiu@chengyiqiu:~/Envs$

发现使用pip装包时会报错：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
p.linux-aarch64-cpython-38/psutil/_psutil_common.o
      psutil/_psutil_common.c:9:10: fatal error: Python.h: No such file or directory
          9 | #include <Python.h>
            |          ^~~~~~~~~~
      compilation terminated.
      psutil could not be installed from sources. Perhaps Python header files are not installed. Try running:
        sudo apt-get install gcc python3-dev
      error: command '/usr/bin/aarch64-linux-gnu-gcc' failed with exit code 1
      [end of output]

  note: This error originates from a subprocess, and is likely not a problem with pip.
  ERROR: Failed building wheel for psutil
Failed to build psutil
ERROR: Could not build wheels for psutil, which is required to install pyproject.toml-based projects

然后尝试安装：

1
sudo apt-get install python3.8-dev

成功了！

因此，当所有步骤为：

1
2
3
4
5
6
sudo add-apt-repository ppa:deadsnakes/ppa
sudo apt-get update
# 下次创建新环境直接从这儿开始
sudo apt install python3.8
sudo apt install python3.8-distutils
sudo apt-get install python3.8-dev

打包requirement.txt：

1
pip list --format=freeze > requirements.txt

开swap

首先要得到在哪个盘上开swap，输入df，然后最后有/的表示有充足的空间开swap：

1
2
3
4
5
6
7
8
chengyiqiu@chengyiqiu:~/myswapfile$ df -m
Filesystem     1M-blocks  Used Available Use% Mounted on
tmpfs                380     4       376   1% /run
/dev/mmcblk0p2    116950 11578    100565  11% /
tmpfs               1896     0      1896   0% /dev/shm
tmpfs                  5     0         5   0% /run/lock
/dev/mmcblk0p1       253   149       104  60% /boot/firmware
tmpfs                380     1       380   1% /run/user/1000

然后选择mmcblk0p2：

1
2
3
4
5
6
7
8
9
10
11
mkdir myswapfile
cd myswapfile/
sudo dd if=/dev/mmcblk0p2 of=swapfile bs=1G count=4
sudo chmod 600 swapfile
sudo mkswap swapfile
sudo swapon swapfile
free -m

               total        used        free      shared  buff/cache   available
Mem:            3790         494        1081           3        2213        3098
Swap:           4095           0        4095

在服务器上（2G memory）经历过一次pip torch的时候被kill掉，原因就是爆内存了（OOM），这时可以通过开swap来解决。

做毕设的时候使用的python的后端框架flask，在读取大文件csv数据集时，也是因为OOM导致python进程被莫名其妙的杀掉了，应该也可以采取开swap的方法。

htop

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
以下是CPU度量指标的颜色编码。

蓝色：显示低优先级进程使用的CPU的百分比。

绿色：显示普通用户拥有的进程使用的CPU的百分比。

红色：显示系统进程使用的CPU的百分比。

青色：显示Steal时间使用的CPU的百分比。

以下是内存度量指标的颜色编码。

绿色：显示已使用内存的百分比。

蓝色：显示已使用缓冲区的百分比。

橙色：显示已使用缓存的百分比。

以下是SWAP度量指标的颜色编码。

红色：显示已使用SWAP内存的百分比。

线性神经网络

线性回归

线性回归严格来说是一种仿射变换（affine transformation）：将特征通过加权（乘以参数w）然后再进行线性变换，最后通过偏置项（b）进行平移。

对于一个特定的样本，线性回归可表示为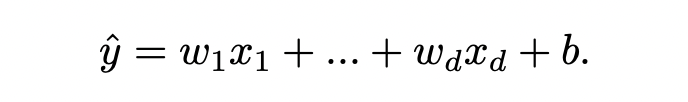：![截屏2023-07-31 20.43.26](./d2l/截屏2023-07-31 20.43.26.png)

写成向量的形式就是（向量和向量之间的点积）：

![截屏2023-07-31 20.44.01](./d2l/截屏2023-07-31 20.44.01.png)

dl中读入的数据集一般都是矩阵，很多样本的集合，所以可以直接写成矩阵的形式。那么就是写成向量和矩阵的乘法形式：

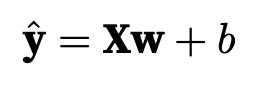
![截屏2023-07-31 20.45.18](./d2l/截屏2023-07-31 20.45.18.png)

线性回归模型比较特殊，因为其有解析解，能通过数学的方法求出解的表达式：

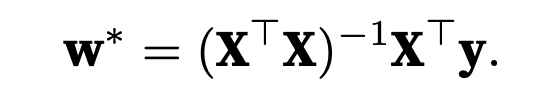
![截屏2023-07-31 21.14.07](./d2l/截屏2023-07-31 21.14.07.png)

这是一个模型的优化思路，但绝大部分模型没有解析解（就算有，通过数学来求得解析解可能可行，但计算量特别大）。于是我们在没有解析解的情况下，可以通过从大量数据中，使用梯度下降（gradient descent），得到数值解。

从整个数据集中随机取出一个batch size大小的数据，然后求loss，最后再反向传播更新参数，过程如下：

  • (1)初始化模型参数的值，如随机初始化;
  • (2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。对于平方损失和仿射变换，我们可以明确地写成如下形式:

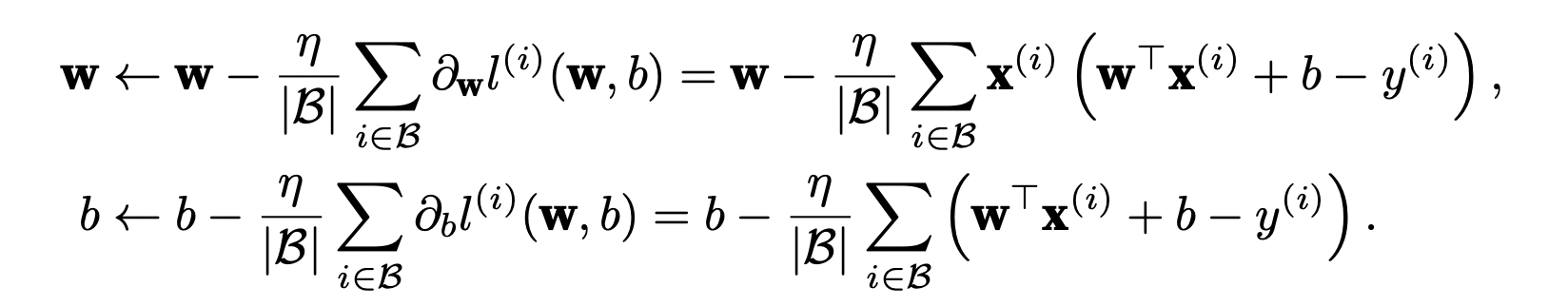
![截屏2023-07-31 21.18.59](./d2l/截屏2023-07-31 21.18.59.png)

线性回归可以看作为单层神经网络，因为输入层不进行计算，整个网络的计算神经元只有一个，一层，所以称为单层神经网络。该网络的特征纬度为d，标签维度为1。

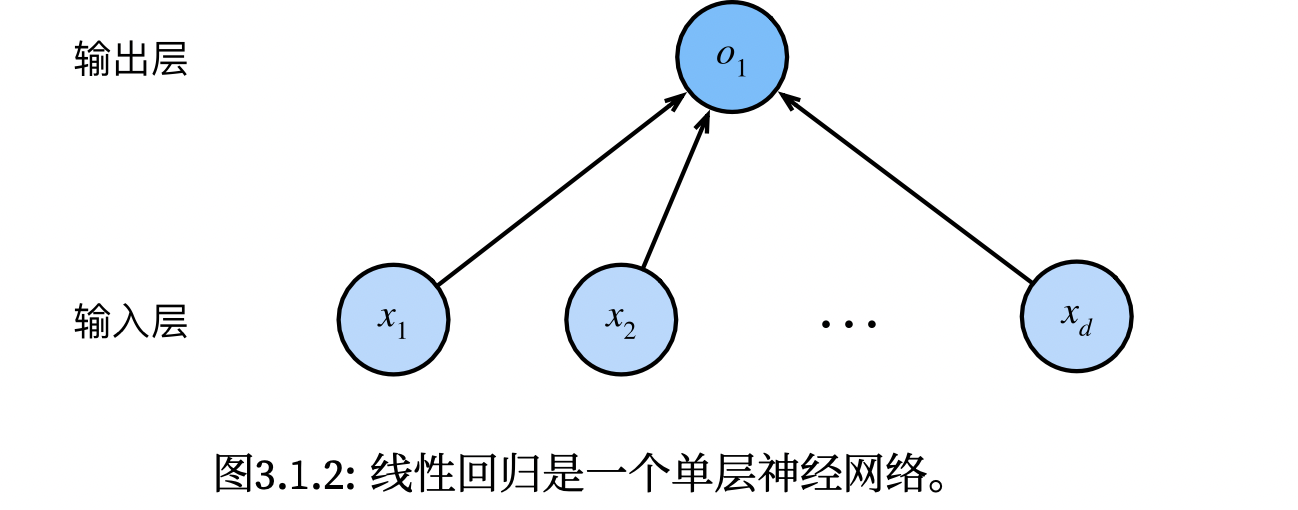
![截屏2023-07-31 23.38.10](./d2l/截屏2023-07-31 23.38.10.png)

DL启发于神经学，但更多的灵感 源自数学、统计、计算机。

![截屏2023-07-31 23.44.44](./d2l/截屏2023-07-31 23.44.44.png)

线性回归从0开始中，有一段代码是手动生成的迭代器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        print(batch_indices) # 从数据集中选取了一组batch size大小的index
        yield features[batch_indices], labels[batch_indices] # tensor可以采取这种读的方式，tensor里面套tensor类型的index

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

这种方式实现的迭代器能使用，但是由于是随机读取一个batch size大小的数据，会用到很多次随机读取内存，这样有悖于局部性原理，时间较长性能较差。后续用到的框架中的迭代器就没有这个问题，

下面使用的代码，是利用torch中的normal函数来生成原始参数，原始参数服从正态分布，均值为0标准差为0.01，可以指定数据的维度：

1
2
3
4
import torch

w = torch.normal(0, 0.01, size=(199, 222, 123, 101), requires_grad=True)
print(w)

线性回归的简洁实现中，有这么一段代码，里面有一个*，没见过：

1
2
3
4
5
6
7
8
9
def load_array(data_arrays, batch_size, is_train=True):  
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train) # shuffle洗纸牌，表示随机打乱

batch_size = 10
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter))

这个不能去掉，他的意义是：括号中的一个星号，表示对list解开入参，即把列表元素分别当作参数传入*

下面是一个简单的例子，输出是10：

1
2
3
4
5
6
def add(a, b, c, d):
    return a + b + c + d


arr = [1, 2, 3, 4]
print(add(*arr))

softmax回归

回归可以用来预测连续值，而分类问题也可以转化为回归问题，下面的图就可以看出，分类问题就是多了几个输出的结点。

回归到具体分类问题上：一张照片四个像素，可能是猫、狗、鸡。也就是：4个特征，3个标签。四个特征好量化，可以直接写成向量形式；但是标签怎么转变为数据呢，很容易就能想到[1, 2, 3]的形式，但是这样编码是有递增的自然顺序，但是显示数据中的标签并没有自然顺序，因此，采用独热编码（one hot encoding）的形式：

1
2
3
猫：[1, 0, 0]
狗：[0, 1, 0]
鸡：[0, 0, 1]

多层感知机

感知机

下面是一个4层的感知机，中间有三个隐藏层，神经元的个数分别为：5，3，2。特征维度为4，标签维度为2。

可以看到从输入到第一层隐藏层，是增加了1的，然后是逐层递减。也可以直接开始递减。

为什么要这样做，里面是有工程经验的：深度学习本质上是一个压缩信息量的过程（回顾周志华老师的机器学习的课程，信息量是在逐层递减），隐藏层有三层，神经元的个数在递减，代表着数据中的信息量也是在递减的，最终到输出层。我们可以选择：

  • 只用一个隐藏层，但神经元个数非常多，如128，256（宽度学习doge）。
  • 像下图一样神经元逐渐递减，每层都学一点东西。

但是层数一定不能太深，并且层与层之间的神经元个数也不能衰减太快，不然整个网络可能坍塌，丢失掉重要的信息。

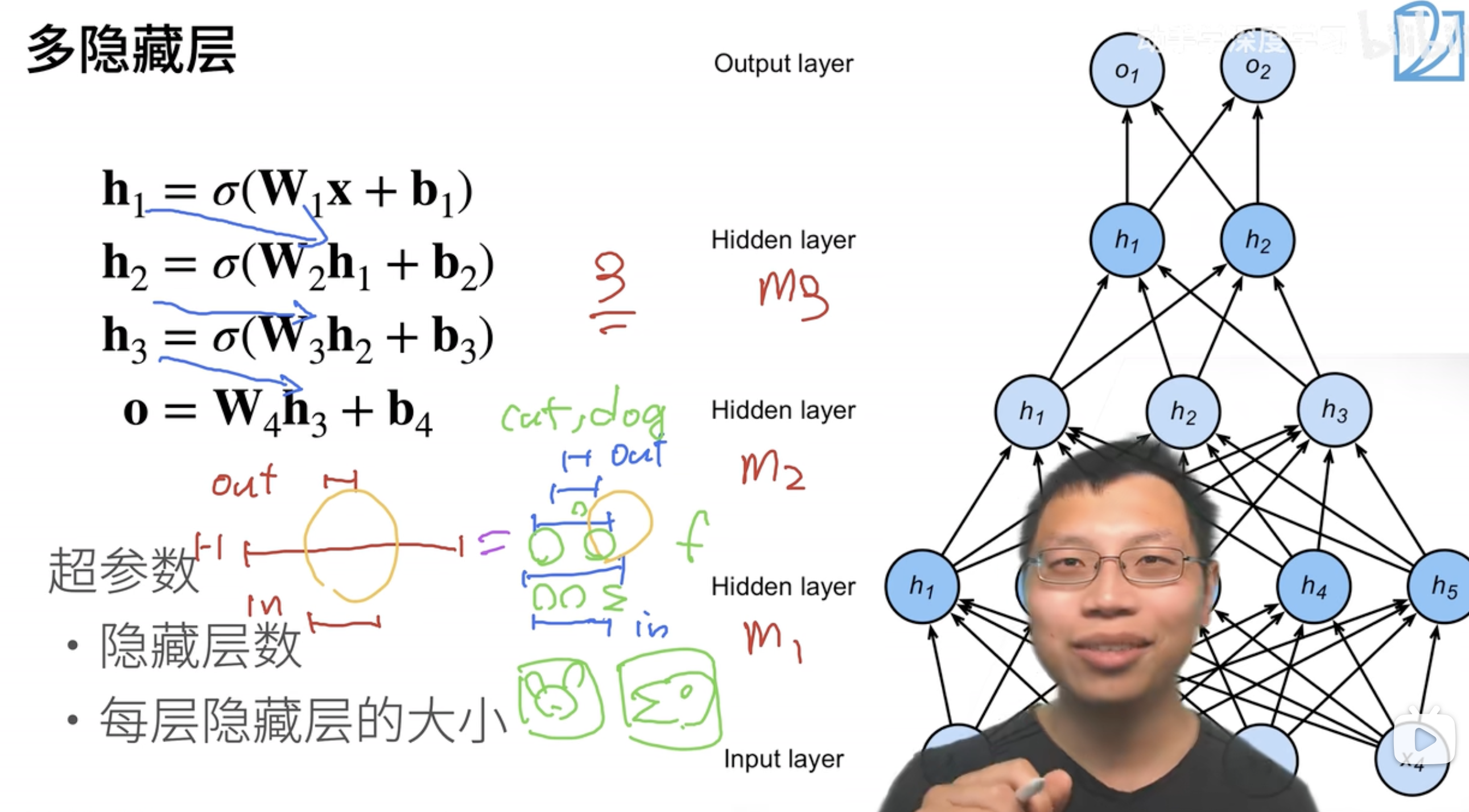
![截屏2023-08-01 20.53.22](./d2l/截屏2023-08-01 21.53.34.png)

至于最后为什么我们选择的是深度学习而不是宽度学习（浅度学习），原因就是浅度学习并不好做：

  • 从人的直观上来讲，很难一口吃个胖子，学东西都是慢慢学，所以我们的网络每层都学一点东西，最后模型收敛。
  • 从计算机的角度，只用一个隐藏层就将所有信息学到，这样难度很大，很难计算出来，也很难去调度所有的神经元应该怎么学（毕竟是黑盒）。

激活函数

激活函数的存在使得我们的mlp不再是仿射变化套娃仿射变换，当我们使用非线性的激活函数时，我们的模型就不会退化为仿射变换了。

  • 只有隐藏层才会加激活函数，输出层不会加激活函数
  • 箭头->神经元+激活函数，这属于一个隐藏层
  • 箭头->输出结点，输入输出层

我们的模型长这样：

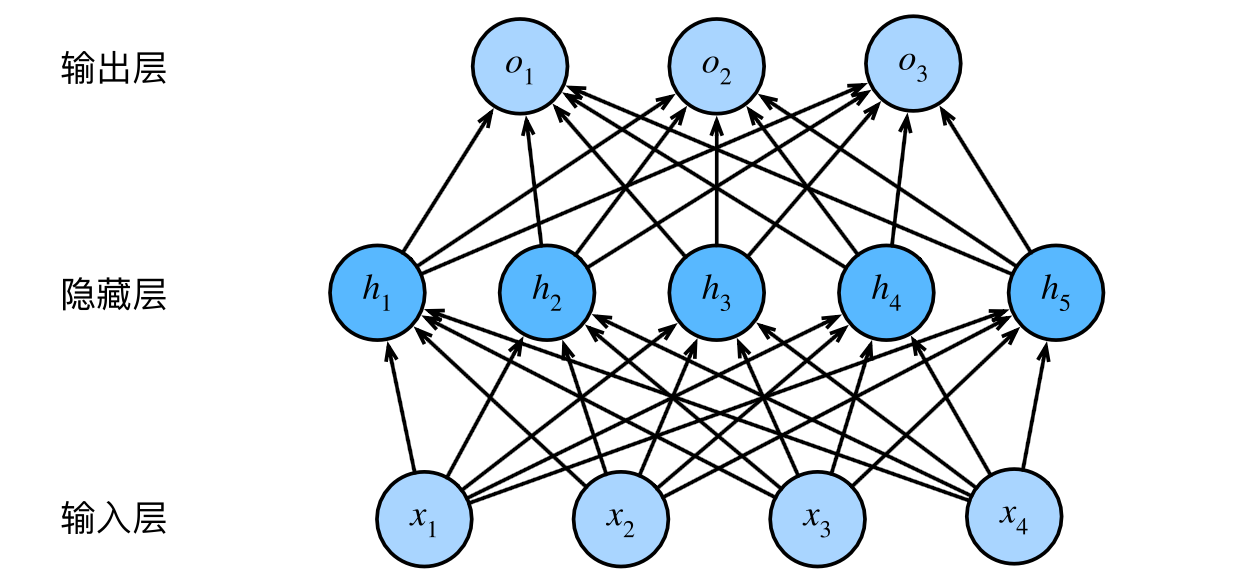
![截屏2023-08-04 12.52.27](./d2l/截屏2023-08-04 12.52.27.png)

从下面这样：

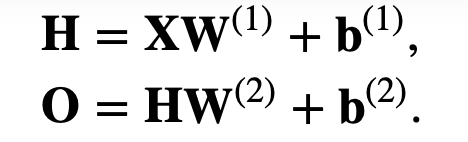
![截屏2023-08-04 12.51.36](./d2l/截屏2023-08-04 12.51.36.png)

变成了：

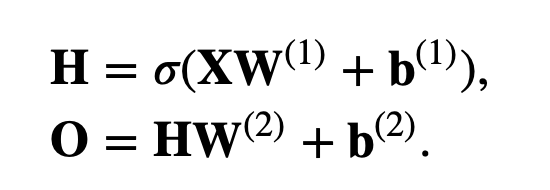
![截屏2023-08-04 12.51.59](./d2l/截屏2023-08-04 12.51.59.png)

ReLU

激活函数的意义在于将线性变为非线性，钟爱ReLU函数的很大一个原因是：简单。像其他两个函数里面都要做至少一次指数运算。而在CPU上，做一次指数运算的时间可以做十万次乘法运算！代价非常昂贵！而GPU中有相应的运算单元，比CPU就好很多了。

ReLU的函数图如下：

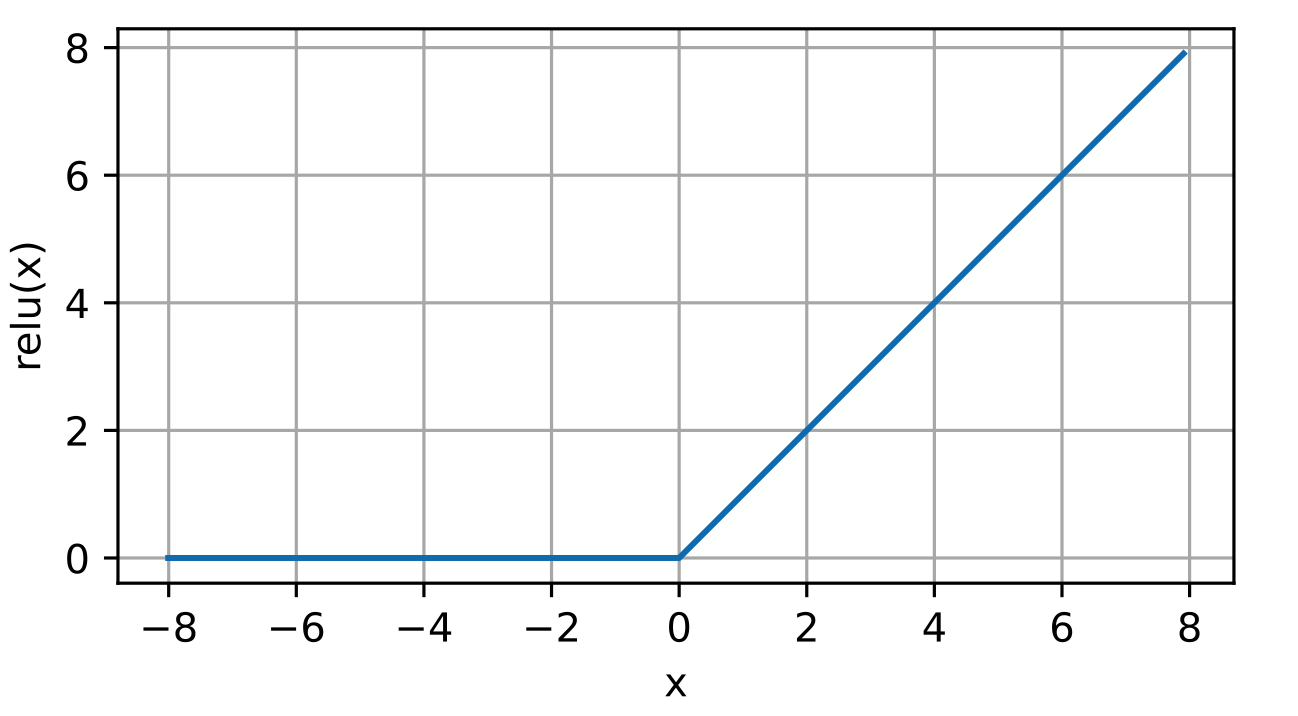
![截屏2023-08-04 12.58.14](./d2l/截屏2023-08-04 12.58.14.png)

可以看到ReLU在0点不可导，我们默认使用0点的倒数为0（其实介于0和1之间都可以，对于这种边界的不可导点）但是，现实中不会出现输入为0的情况，有一句谚语：如果微妙的边界条件很重要，我们很可能是在研究数学而非工程。

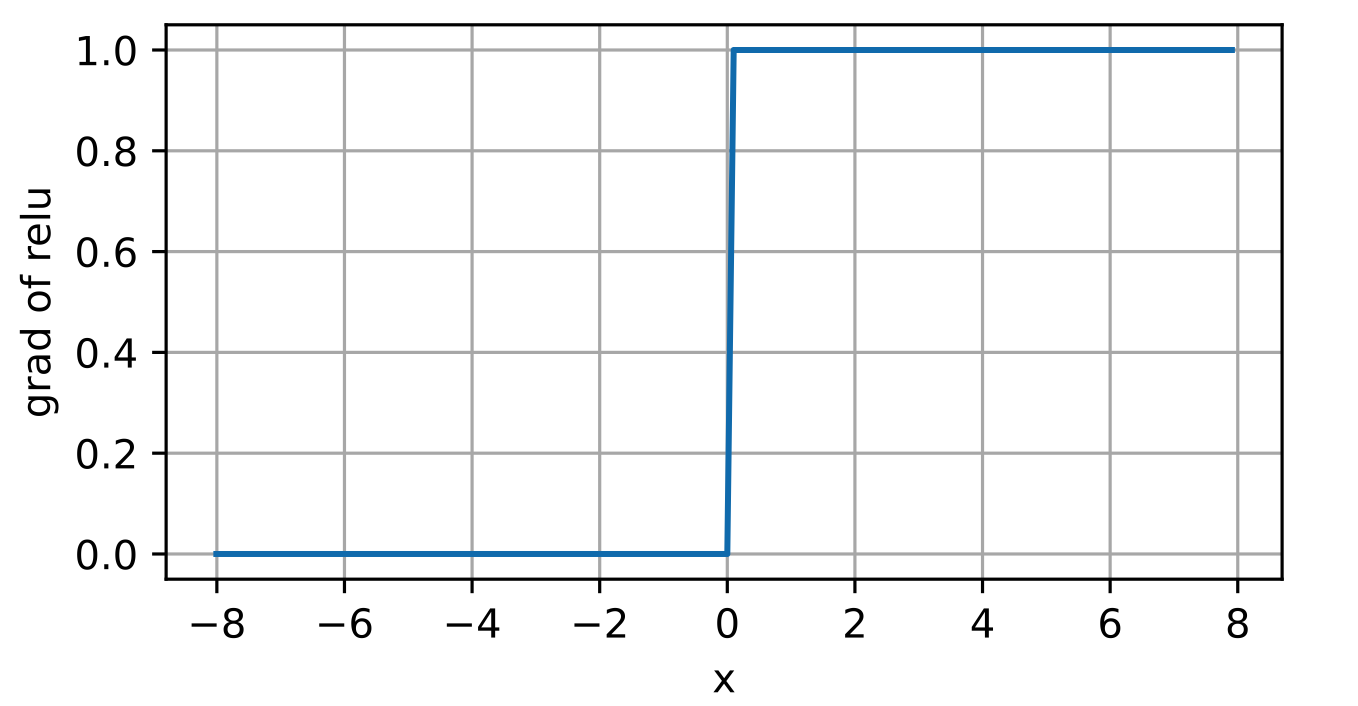
![截屏2023-08-04 13.01.52](./d2l/截屏2023-08-04 13.01.52.png)

ReLU还有一些变体：即使参数是负的，某些信息仍然可以通过

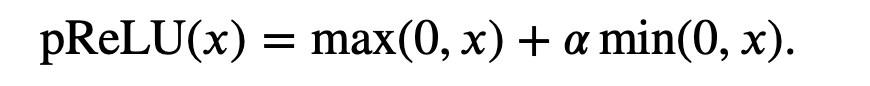
![截屏2023-08-04 13.03.06](./d2l/截屏2023-08-04 13.03.06.png)

sigmoid

表达式：
$$
sigmoid(x)=\frac{1}{1+e^{-x}}
$$
图：

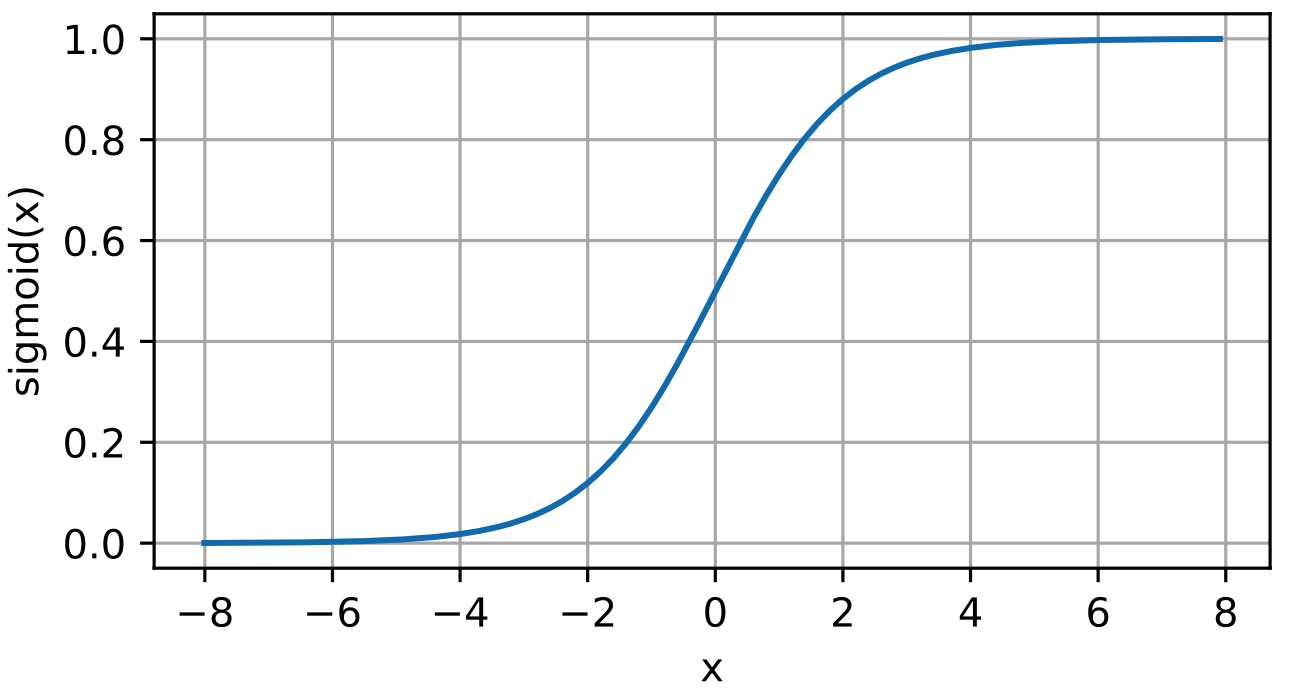
![截屏2023-08-04 13.07.18](./d2l/截屏2023-08-04 13.07.18.png)

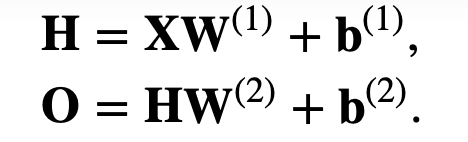
![截屏2023-08-04 12.51.36](./d2l/截屏2023-08-04 12.51.36-1125646.png)

sigmoid有一个特性是：求导之后刚好可以表达成正例反例
$$
\frac{d}{dx}sigmoid(x)=sigmoid(x)(1-sigmoid(x))
$$
导数图像：

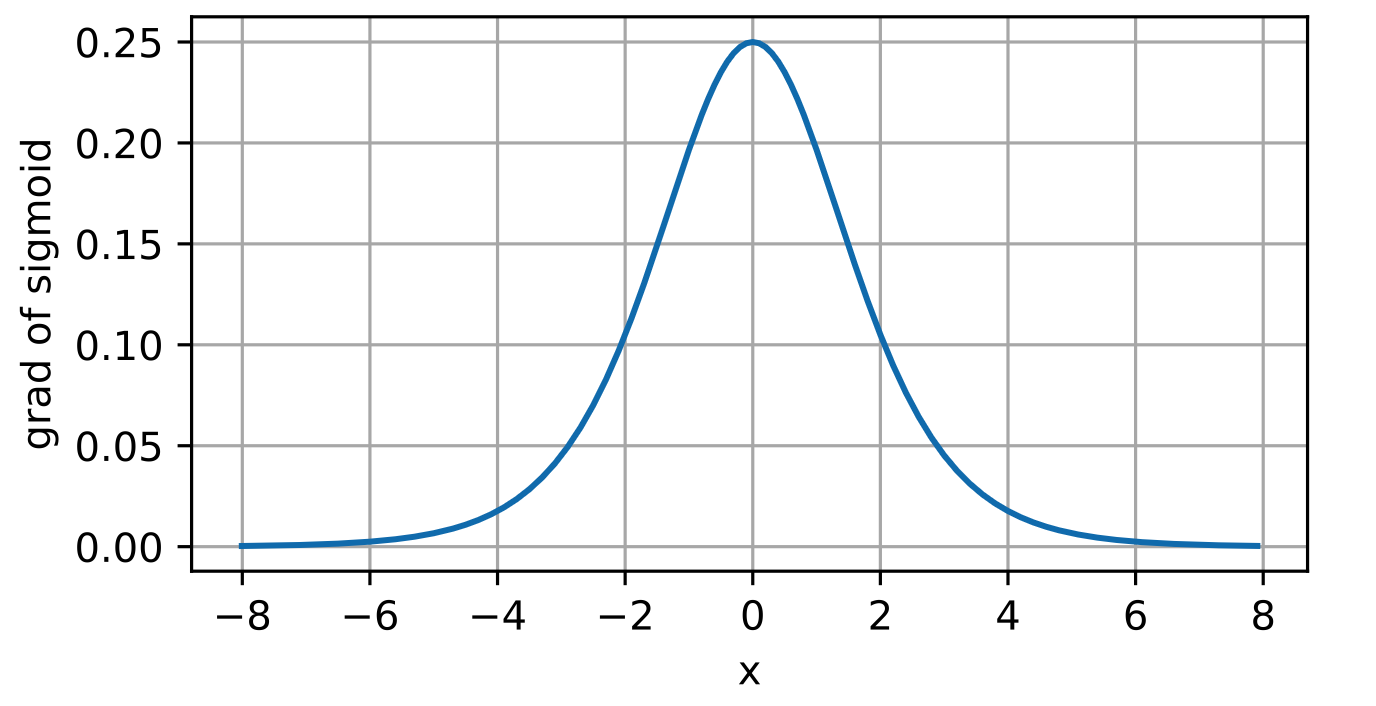
![截屏2023-08-04 13.12.16](./d2l/截屏2023-08-04 13.12.16.png)

tanh

表达式：
$$
tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}
$$
图：

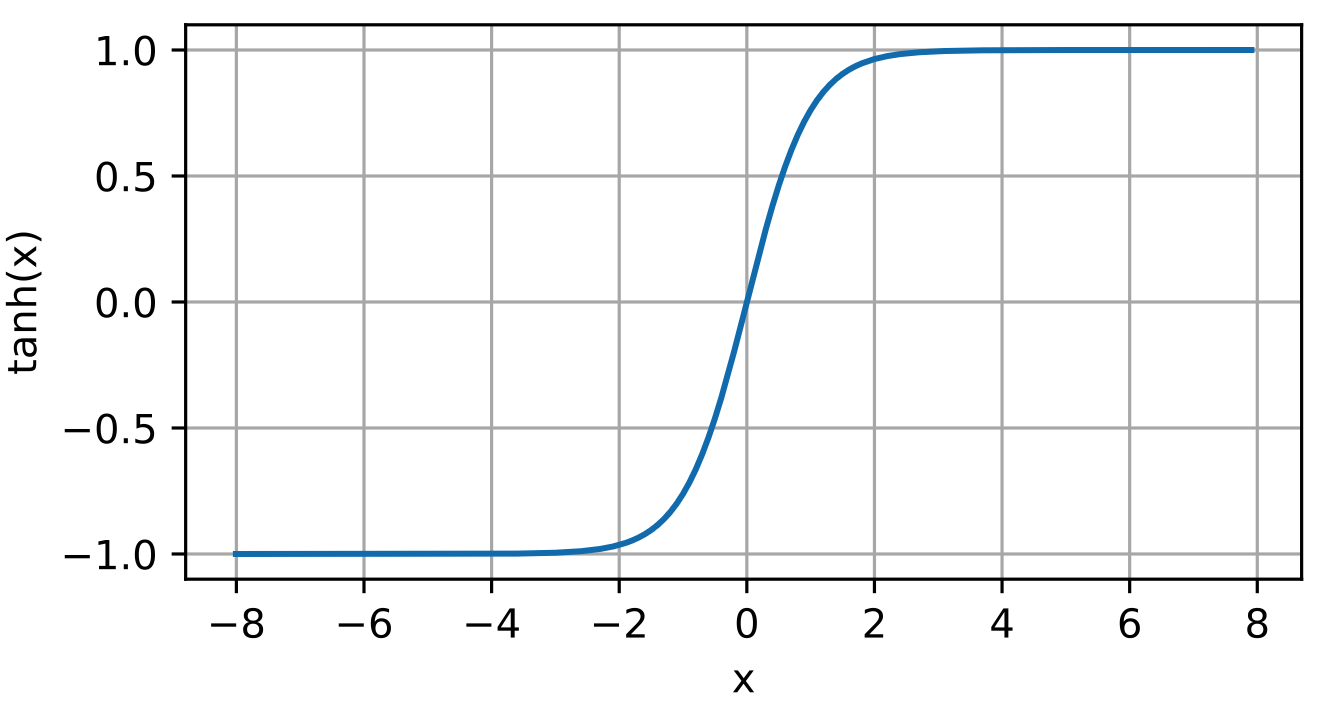
![截屏2023-08-04 13.13.56](./d2l/截屏2023-08-04 13.13.56.png)

导数：
$$
\frac{d}{dx}tanh(x)=1-tanh^2(x)
$$

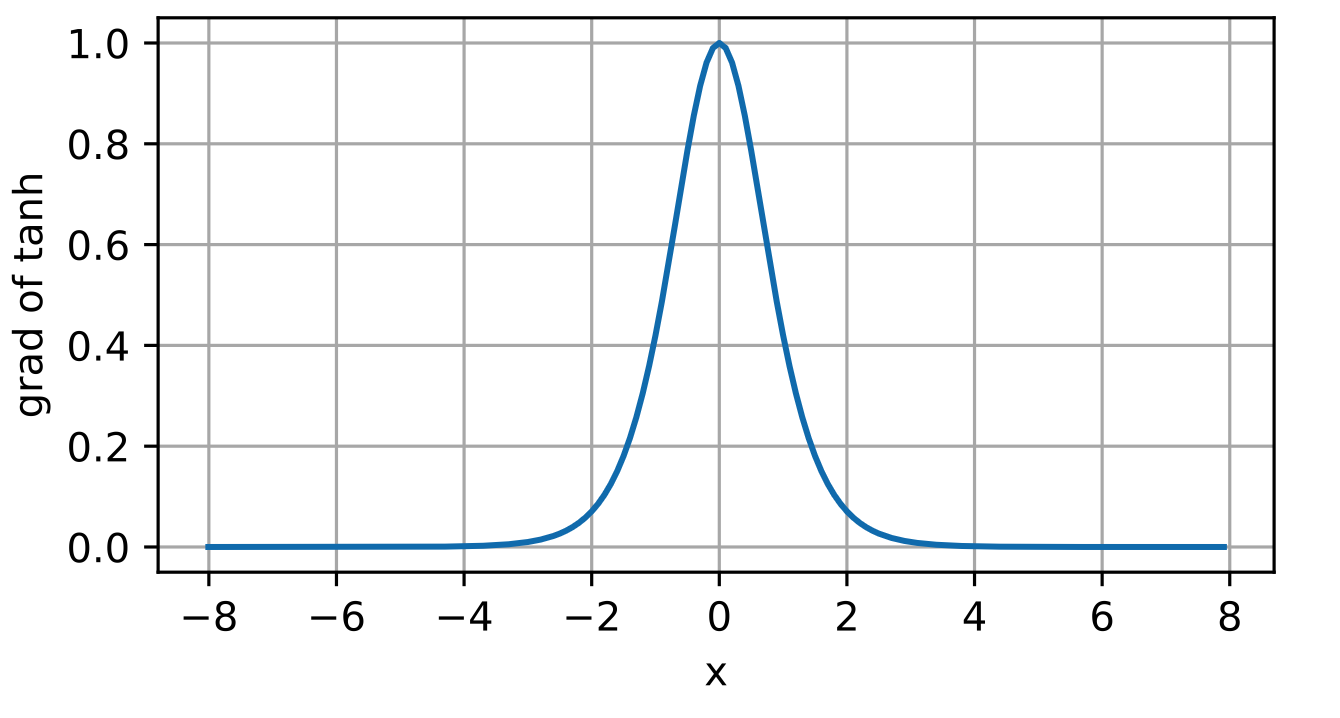
![截屏2023-08-04 13.14.59](./d2l/截屏2023-08-04 13.14.59.png)

模型选择、欠拟合、过拟合

用于对抗过拟合的技术叫做正则化。

统计学习理论

一般情况我们假设我们抽取的数据是服从独立同分布的，也就是说2、3样本存在的相关性并不比2、200000两个样本的相关性强（和索引、抽取顺序无关）。但是这种假设很容易就被推翻，很容易找到假设失效的情况。

如果我们根据从加州大学旧金山分校医学中心的患者数据训练死亡风险预测模型， 并将其应用于马萨诸塞州综合医院的患者数据，结果会怎么样？ 这两个数据的分布可能不完全一样（可能有空间相关）。 此外，抽样过程可能与时间有关。 比如当我们对微博的主题进行分类时， 新闻周期会使得正在讨论的话题产生时间依赖性，从而违反独立性假设。

模型复杂性

对于一个分类模型，VC等于一个最大的数据集的大小，不管如何给定标号（label），都存在一个模型来对它进行完美分类

可以计算出线性分类器的VC维：

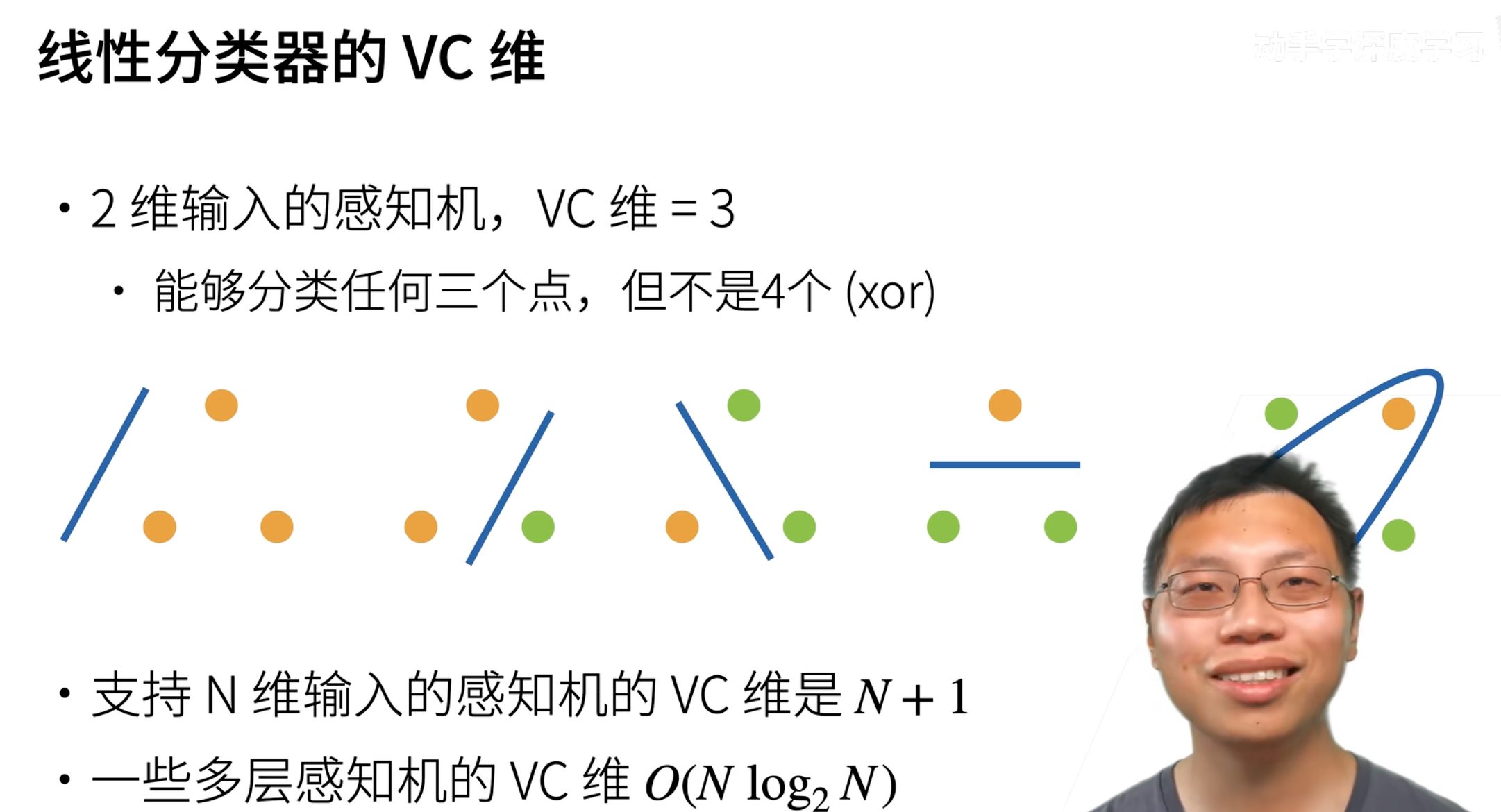
![截屏2023-08-04 15.12.36](./d2l/截屏2023-08-04 15.12.36.png)

模型容量和数据大小的关系如下：

  • 模型容量很低（比较简单），但是数据集比较大时，其实是学不到什么东西的，所以是欠拟合
  • 模型容量很高（神经元多，复杂），但是数据集比较小的时候，就很容易把噪声学进去，也就是容易过拟合。

一般第二种情况比较常见，也就是很容易过拟合：比如给一组线性的数据，然后放入三四层的感知机里面去训练，很容易就把噪声当作数据的规律了，导致过拟合。

![截屏2023-08-02 14.46.35](./d2l/截屏2023-08-02 14.46.35.png)

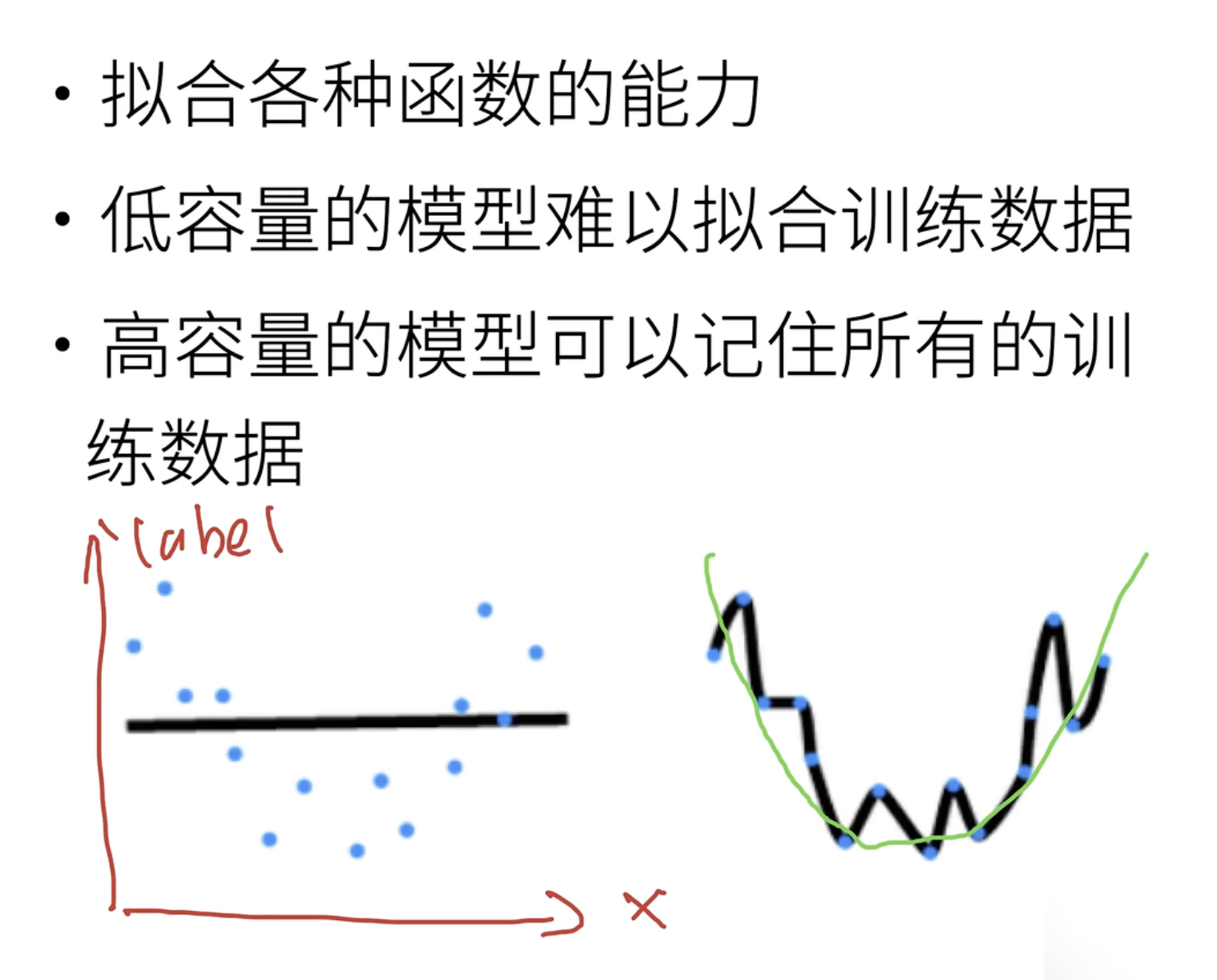
模型容量还可以定义为：拟合各种函数的能力。

下面对于同样的数据集，左边的模型比较简单，因此只学到了线性；而右边的模型比较复杂，学成了一个非常复杂的函数。

但事实上，这些数据服从的是一个二次函数的分布，

因此，从数据集的大小上我们能够感受到数据的复杂与否，然后再选择合适的模型来训练。

![截屏2023-08-02 14.50.41](./d2l/截屏2023-08-02 14.50.41.png)

![截屏2023-08-03 09.27.21](./d2l/截屏2023-08-03 09.27.21.png)

最后是书中的经验，哪些因素会影响模型泛化：

  1. 可调整参数的数量。当可调整参数的数量（有时称为自由度）很大时，模型往往更容易过拟合。
  2. 参数采用的值。当权重的取值范围较大时，模型可能更容易过拟合。
  3. 训练样本的数量。即使模型很简单，也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。PS：也就是说还是得根据数据来选择模型

验证集

神经网络中的w和b是在train set上训练出来的，而神经网络层数、神经元个数则是我们指定的超参数（这些东西对我们的模型容量有影响）。调整超参数有助于我们得到更适合我们数据的模型。

但是train set是用来调整参数，test set是用来测试训练出来的模型，都不好直接拿来调整超参数。因此，在数据集上再次划分一块出来，作为验证集，用来调整超参数。

因此，将我们的数据分成三份， 除了训练和测试数据集之外，还增加一个验证数据集（validation dataset）， 也叫验证集（validation set）

欠拟合和过拟合

下面是原书中的观点，在现实训练中的过拟合和欠拟合。

当我们比较训练和验证误差时，我们要注意两种常见的情况。 首先，我们要注意这样的情况：训练误差和验证误差都很严重， 但它们之间仅有一点差距。 如果模型不能降低训练误差，这可能意味着模型过于简单（即表达能力不足）， 无法捕获试图学习的模式。 此外，由于我们的训练和验证误差之间的泛化误差很小， 我们有理由相信可以用一个更复杂的模型降低训练误差。 这种现象被称为欠拟合（underfitting）。

另一方面，当我们的训练误差明显低于验证误差时要小心， 这表明严重的过拟合（overfitting）。 注意，过拟合并不总是一件坏事。 特别是在深度学习领域，众所周知， 最好的预测模型在训练数据上的表现往往比在保留（验证）数据上好得多。 最终，我们通常更关心验证误差，而不是训练误差和验证误差之间的差距。

权重衰减

范数

一般使用L2范数来约束w，作为特征向量的惩罚。在原本的loss上，加上L2范数
$$
L(w,b)+\frac{\lambda}{2}||w||^2
$$
当$\lambda=0$时，恢复成了原来的损失函数；当$\lambda>$0时，就会对w进行惩罚：
$$
w<-(1-n\lambda)w-\frac{\eta}{\beta}\sum_{\beta}x^{i}(w^Tx^{(i)}+b-y^{(i)})
$$
表现出来就是：如果w变大太大了，那么L2范数就会把往小了拉。

至于L1范数，二者有不同的用途：

  • L2范数对权重向量的大分量施加了巨大的惩罚。因此学习算法倾向于“在大量特征上均匀分布权重的模型”。
  • L1范数会导致模型将权重集中在一小部分特征上， 而将其他权重清除为零（特征选择）

暂退法（Dropout）

过拟合

我们还是从线性模型出发。当样本很少、特征很多的时候，我们多跑几轮epoch，很可能就会过拟合；相反， 当特征数很少，而样本足够多时，这时就并不容易过拟合了。但是其代价是：只会关注样本的某几个特征，而不会关注这些特征之间的联系。

而神经网络就相反了，神经网络并不关注单个的特征，而是关注特征与特征之间的联系，举个例子：“神经网络可能推断“尼日利亚”和“西联汇款”一起出现在电子邮件中表示垃圾邮件， 但单独出现则不表示垃圾邮件。”但是正是由于这个，当我们有过多的样本时，就很容哦过拟合（特征之间明明没有关系，但是模型会误认为噪声是某种特种之间的关系，尤其是当阶数变高时）

稳健性

一个好的模型应该具有以下特点：

  • 模型简单，换言之就是模型的维度不应该太高
  • 最终的模型应该比较平滑，也就是说对于样本有一定噪声的情况下能给出同样的输出。

上面两点可以归结成模型的稳定性。

暂退法可以增加模型的稳健性，从下面两个方面：

  • 在中间的隐藏层与层之间，加入噪声。这样从输入输出的角度来看，模型会比较平滑。
  • 忽略隐藏层中的某些神经元节点

![截屏2023-08-07 13.13.49](./d2l/截屏2023-08-07 13.13.49.png)

如上，毕晓普的方法就是给隐藏层加入噪声；而标准的dropout则是丢弃某些神经元的结点，如下：

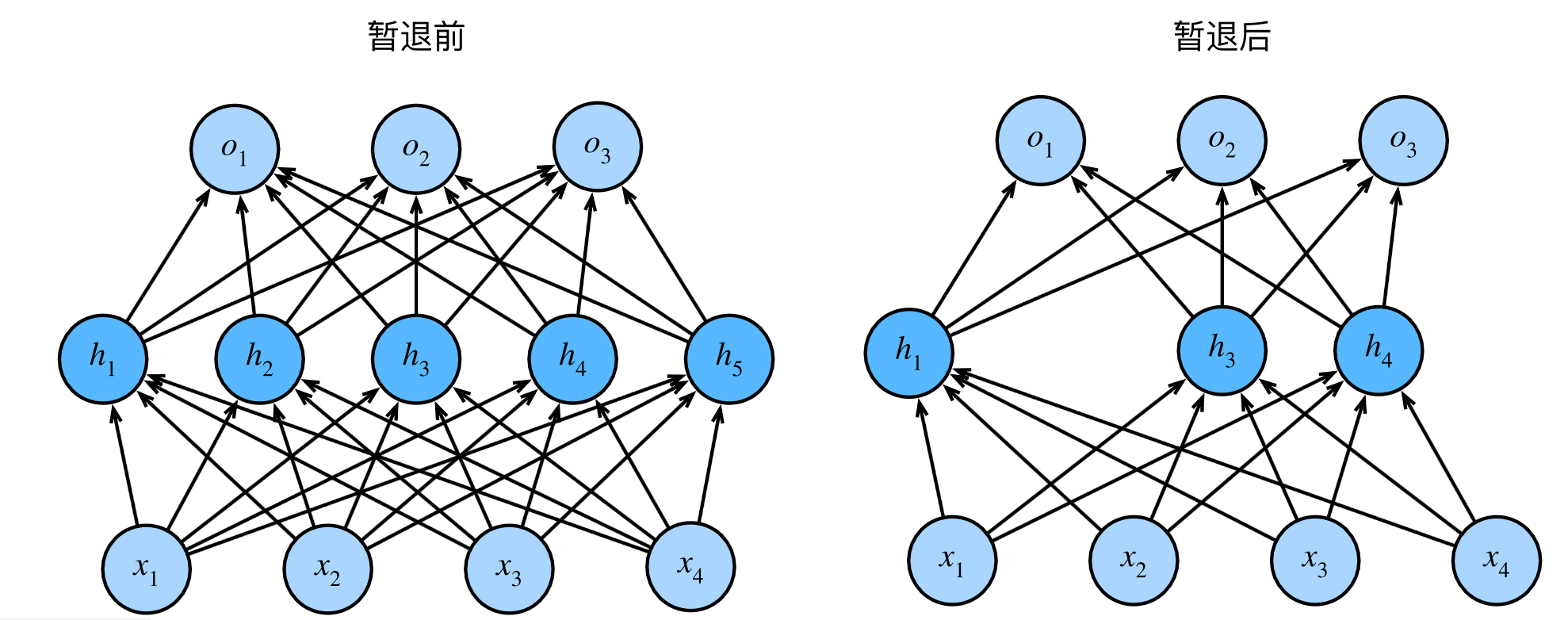
![截屏2023-08-07 13.15.35](./d2l/截屏2023-08-07 13.15.35.png)

前向传播、反向传播、计算图

前向传播

定义：从输入层，到输出层，计算和存储神经网络中每层的结果。

首先是输入到第一个隐藏层：
$$
z=w_1x \
h_1=\phi(z)
$$
然后就是隐藏层到输出层
$$
o=W_2h \
L=l(o,y)
$$
再加上L2范数
$$
s=\frac{\lambda}{2}(||W_1||^2+||W_2||^2) \
J=L+s
$$
J是最后的目标函数

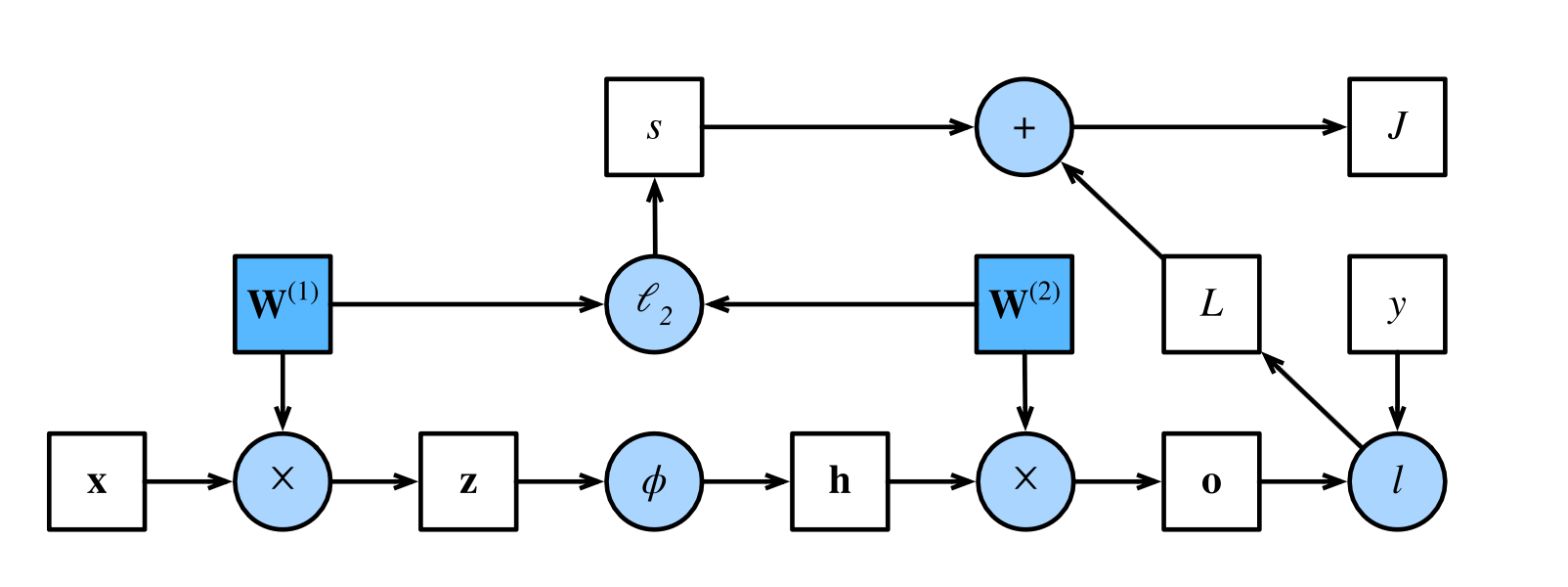
![截屏2023-08-07 15.04.26](./d2l/截屏2023-08-07 15.04.26.png)

反向传播

反向传播就是从结果开始，满满的向前计算偏导数，最后利用链式法则复合到一起，然后得出对参数的梯度。

模型稳定性和模型初始化

数值稳定性和模型初始化

梯度爆炸/消失

参数的初值选取，以及后续激活函数的选定，都对我们模型的训练会造成很大的影响：

  • 参数更新过大，矩阵累乘后会造成梯度爆炸
  • 参数更新过小，会造成梯度消失

还有激活函数，如sigmoid函数，它符合神经学的认知，但是真正放在训练中：

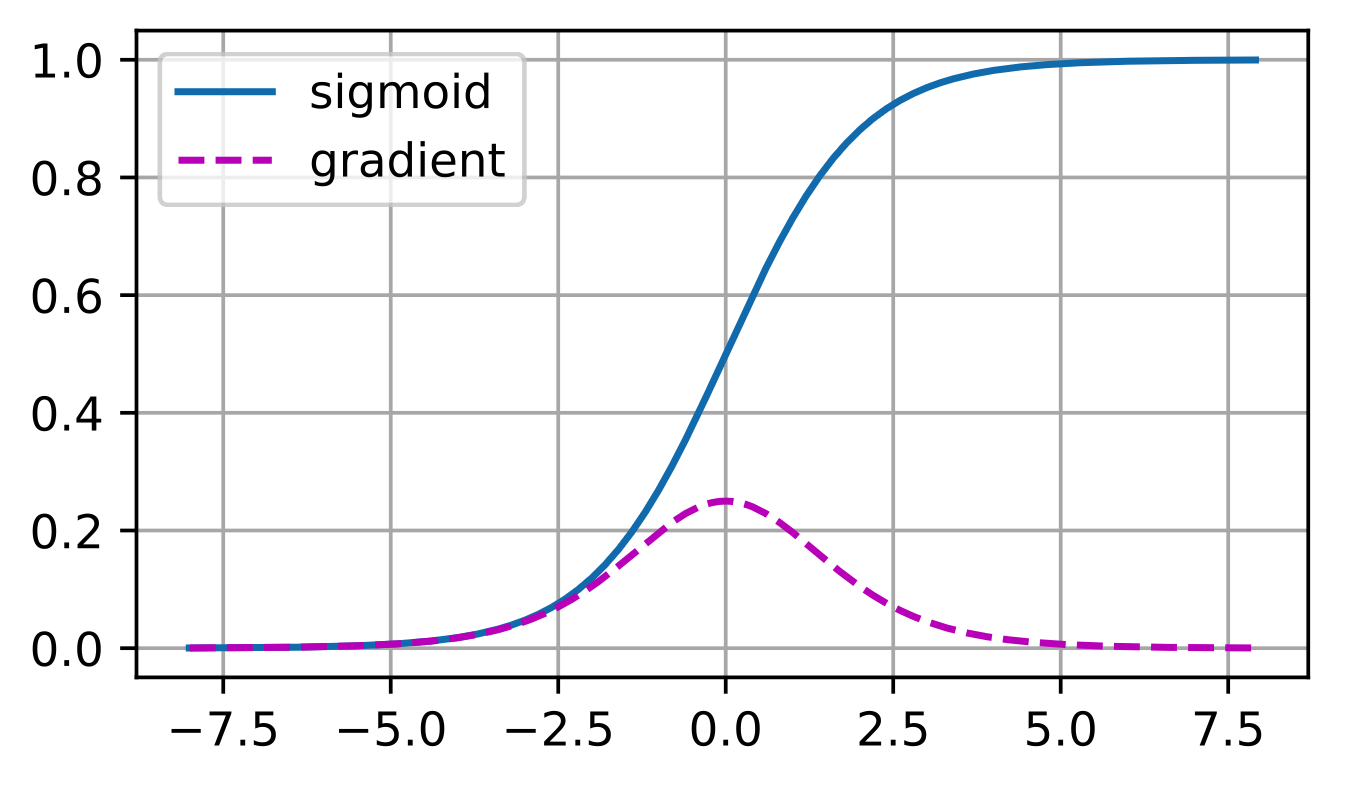
![截屏2023-08-07 19.47.37](./d2l/截屏2023-08-07 19.47.37.png)

当输入过大的时候，sigmoid函数的导数基本为0了，整个的梯度就消失了。

所以现在领域内主要是选择ReLU函数的变体来作为激活函数。

打破对称性

对称性指的是：一个网络中的神经元具有相同的输入、初值权重、激活函数，那么这两个神经元在后续的训练中会保持完全相同的行为，他们的输出完全相同。换句话来说，一个神经元和两个神经元没什么区别。

因此，我们在初始化参数的时候，一定要避免这种情况。

在初始化的时候选择让参数服从一个均值为0方差0.01的正态分布，这样在一定程度上能得到一组较好的参数。

在实际编码时，可以直接选择Xavier初始化。

环境和分布偏移

有一句很好的话：有时模型的部署本身就是扰乱数据分布的催化剂

举个很贴切的例子：假设我们训练了一个贷款申请人违约风险模型，用来预测谁将偿还贷款或违约。 这个模型发现申请人的鞋子与违约风险相关（穿牛津鞋申请人会偿还，穿运动鞋申请人会违约）。 此后，这个模型可能倾向于向所有穿着牛津鞋的申请人发放贷款，并拒绝所有穿着运动鞋的申请人。不久，所有的申请者都会穿牛津鞋，而信用度却没有相应的提高。

上面的例子中，很容易看到：当我们的模型部署后，竟然让数据的分布发生了变化。

协变量偏移

定义：虽然输入的分布可能随时间而改变， 但标签函数（即条件分布𝑃(𝑦∣𝐱)）没有改变。 统计学家称之为协变量偏移（covariate shift）

协变量指的就是特征。

有点抽象，拿一个具体问题举例：

![截屏2023-08-08 15.53.23](./d2l/截屏2023-08-08 15.53.23.png)

训练集是真实的照片，而测试集是卡通照片，对于这种训练集没有这个feature，而测试集有这个feature，可以称为协变量偏移，如果没有办法来适应这个，那么显然，模型会失去应有的效果。

标签偏移

标签偏移刚好和协变量偏移相反。

概念偏移

定义：当标签的定义发生变化时，就会出现这种问题。

听着很奇怪，但举个例子：精神疾病的诊断标准、所谓的时髦、以及工作头衔等等，都是概念偏移的日常映射。随着时间的推移，这些概念的定义可能会发生偏移。

CNN

上一章节所描述的感知机貌似能解决很多问题，例如处理表格类型的数据这种特征数目不是很多的数据集。

但是，假如将我们的输入换成一张1200w*1200w像素的图片，那么按照之前softmax回归的处理思路。将照片的像素平铺成一个一位向量，那么我们就有1万亿个feature，然后第一层隐藏层的神经元个数也为1万亿的话，那么第一层的w就会爆炸，这样训练需要大量的GPU资源，以及人力成本。

因此可以看到，MLP在对于这种图片的处理基本是没什么效果的，因此我们引入卷积神经网络CNN。

从MLP到CNN

卷积本来是在DSP中使用的，FFT中使用，但是由于卷积的两种特性，使得它被运用到DL中，并产生了CNN：

  • 平移不变性：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应
  • 局部性：神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。

互相关运算

其实不应该叫卷积运算，学过DSP里面，卷积的的运算中前面写的是符号，而我们深度学习中，使用的卷积前面的W的索引是正着来的，而数学中的卷积应该是翻着来的，严格的来讲，DL里的卷积应该叫互相关运算

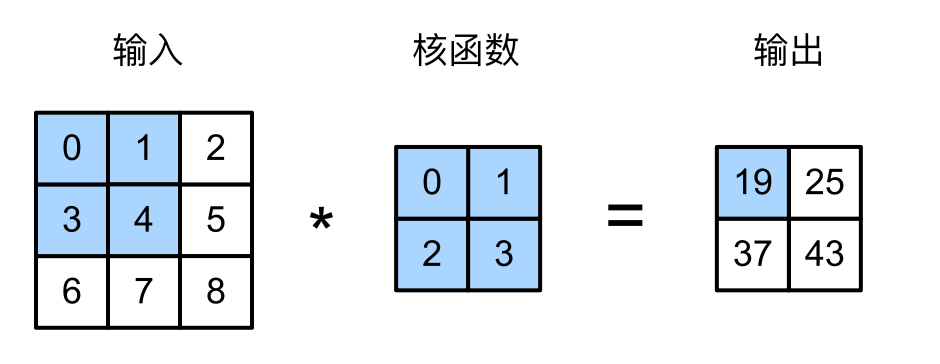
![截屏2023-08-09 10.25.42](./d2l/截屏2023-08-09 10.25.42.png)

假设输入是 $n_hn_w$，然后kernel是$k_hk_w$，那么输出就为：
$$
(n_h-k_h+1)\times(n_w-k_w+1)
$$
下面我们按照书上的内容，手动写一下卷积层，以及对核函数进行一个简单的学习

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import torch
from torch import nn


def get_device():
    return torch.device("mps")


def loss(y_hat, y):
    return 0.5 * ((y_hat - y) ** 2)

def train(net, X, Y, epoch, lr):
    for i in range(epoch):
        Y_hat = net.forward(X)
        l = loss(y_hat=Y_hat, y=Y)
        net.zero_grad()
        l.sum().backward()
        net.weight.data[:] -= lr * net.weight.grad
        print(f'epoch {i + 1}, loss {l.sum():.3f}')


def corr2d(X, K):  # @save
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1), device=get_device())
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y


X = torch.ones((6, 8), device=get_device())
X[:, 2:6] = 0
K = torch.tensor([[1.0, -1.0]], device=get_device())
Y = corr2d(X, K)
net = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False, device=get_device())
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2
epoch = 20
train(net, X, Y, epoch, lr)
print(net.weight.data)


tensor([[[[ 0.9750, -0.9750]]]], device='mps:0')

上面的代码中，我们的net、X、Y、weight、bias都是放在Mac的GPU上的，实际训练也是使用的GPU。

填充和步幅

上面几节讲的CNN中，经过和核函数运算后，我们的输入不断减小，这时有两种情况：

  1. 当我们的输入非常大时，这时可以将我们的网络做的很深，但是仅仅靠核函数带来的线性衰减，我们的信息压缩的非常慢。
  2. 当我们的输入维度很小时，我们靠着线性衰减，我们可能做不了几层，无法把我们的网络做深。

这时候可以对我们的输入做一个填充，并且在和核函数进行运算时，调整我们的步幅。

填充

通常会将我们的填充设置为核函数的维度减一，比如我们是3*3的核函数，那么可以将我们的填充设置为2，这样的话，我们的输入和输出的维度就是一样的了。

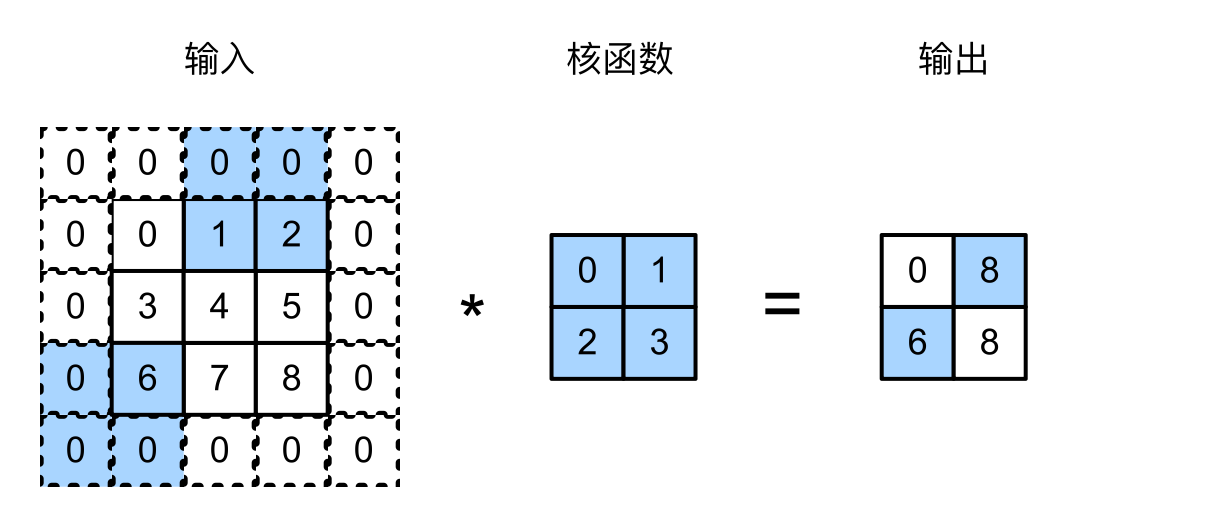
下面的例子中的核函数是大小是2*2的，所以就算填充是1，我们的输入输出维度并没有保持一致。

通常情况我们的卷积核的大小会设置为奇数，好处是：保持空间维度的同时，我们可以在顶部和底部填充相同数量的行

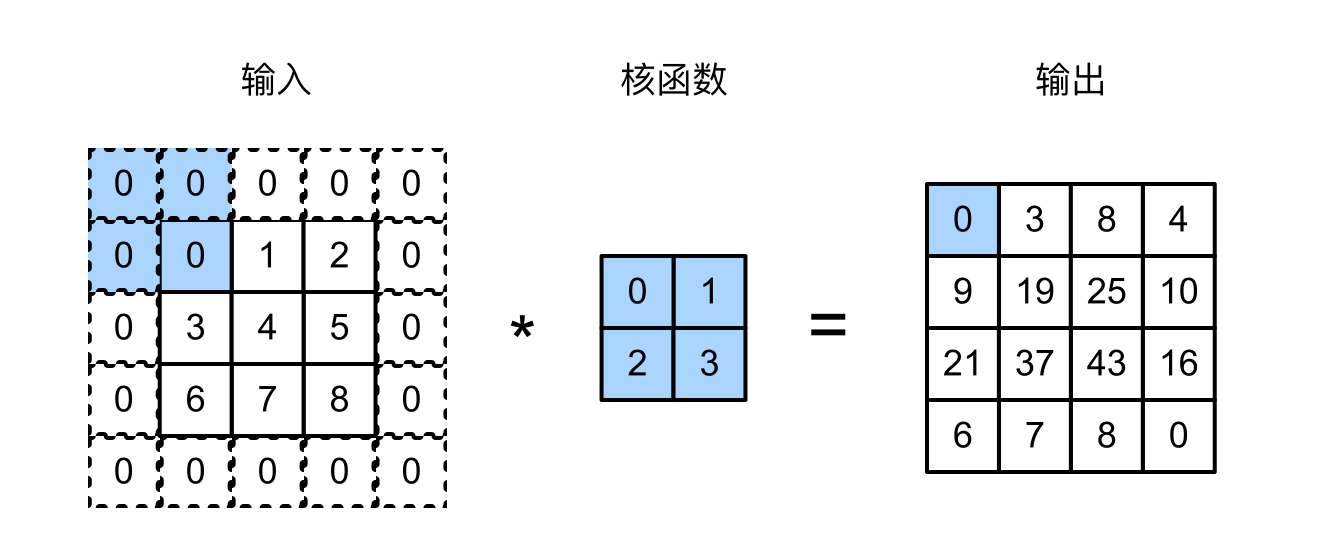![截屏2023-08-09 20.54.35](./d2l/截屏2023-08-09 20.54.35.png)步幅

步幅就是当我们在计算卷积的时候，for loop遍历的步长。一般我们的步幅是1，这样我们的输入和输出之间的关系就是一个线性的衰减了，但为了解决我们刚开始说的输入过大的这种情况，我们可以将步幅设置为2，这样我们的输出相对于输入就会减半，直接从一个线性衰减变成了指数衰减。

![截屏2023-08-09 21.00.15](./d2l/截屏2023-08-09 21.00.15.png)

多输入输出通道

上一节中我们的输入就是一个二维的矩阵，或者说是三维张量，但是现实中我们输入的图片并只是二维张量，例如RGB，每个像素还有红黄蓝三个值可以调，这使得不同程度的红黄蓝比例能够表示各种复杂的颜色。我们说RGB图片有三个通道，当RGB图片作为输入时，我们的输入就是一个$3\times h\times w$的三维张量。

多输入通道

当我们的原始输入是一个RGB图像时，我们的输入就有3个通道，肯定不能用一个卷积核来处理这三个通道，因此，我们需要三个卷积核，做三次互相关运算，然后最终加在一起。

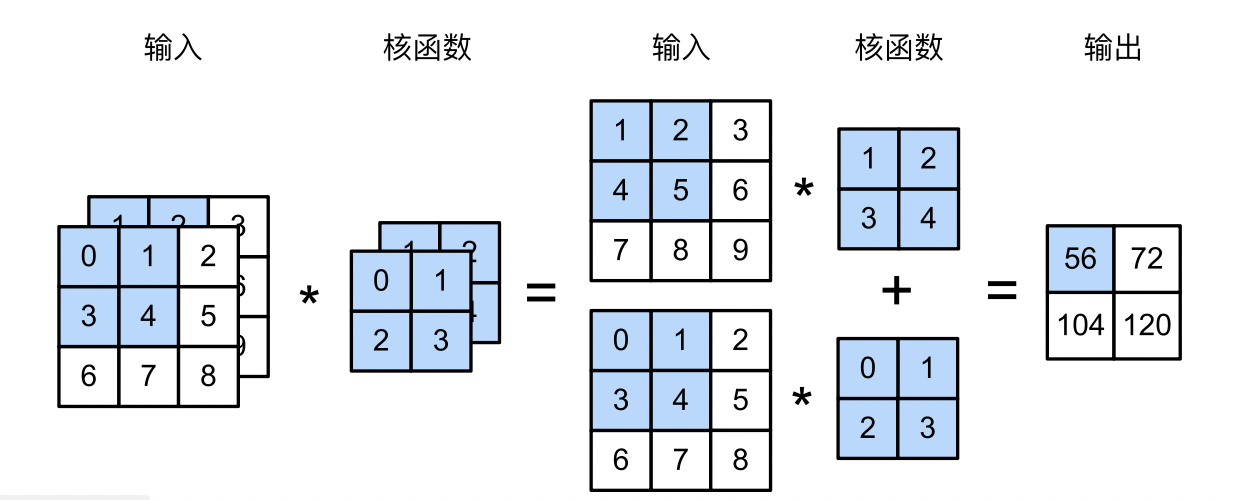
![截屏2023-08-12 19.49.13](./d2l/截屏2023-08-12 19.49.13.png)

上面第一个是第一个卷积层，输入是2通道，所以卷积核也是两个，最后的输出将两个通道的内容合并在了一起，因此输出只有一个通道。

PS：这里每个通道输入和核函数做互相关运算之后，所有通道的结果加在一起了，两个思考：

  • 每个通道输出的结果需不需要乘一个系数，然后再相加到一起？答案是不需要，因为系数可以融进核函数里面，效果是一样的，不需要多此一举
  • 为什么非要用加法操作将每个通道的结果融合在一起？
    • 其一是好算，加法操作比乘法等操作耗时短，卷积层的训练速度加快，这是站在训练的角度。
    • 其二是，每个通道的输出结果其实是一个模式（pattern），把这些模式加在一起能够得出更复杂的模式，至于乘法运算能不能也有很好的效果，就不得而知了

多输出通道

上面有了多输入通道，但是我们的输出还是只是一个二维张量，这样如果作为下一层的输入那么就只有1维了，通道数降低了。

现实中，通道数多的话，能够学习的模式也就多，所以我们希望输出的通道维数也尽可能不要减少，因为神经网络要做很多层可能，如何增加输出通道呢，也很简单：上面有两个卷积核，也就是两个通道，我们可以设置很多卷积核，比如设计100个卷积核，然后分层，每层2个卷积核，一共50层，整个的卷积核的维度就是：$50\times 2\times 2\times2$，前面这个50，代表的就是我们的输出通道数有50个。下面是某层有多个输出通道，卷积核$2\times3\times1\times1$

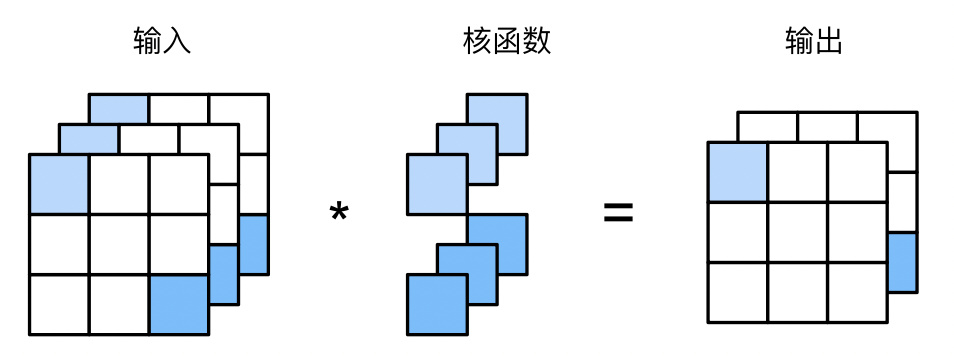
![截屏2023-08-12 20.13.27](./d2l/截屏2023-08-12 20.13.27.png)

$1\times1$卷积核

上图就是$1\times1$的卷积核。这样的卷积核一次只能看一个像素，也就是说失去了其空间能力。

我们之前了解到，从MLP到CNN，就是增加了空间性，所以我们 可以认为：如果某层的卷积核都是$1\times1$的话，那么可视作全连接层，其作用就是融合特征。

汇聚层

汇聚层的目的：

  • 模式融合
  • 降低卷积层对空间信息的敏感性， 增加对平移不变性的支持

我们的卷积层通常是$3\times3$的，，对空间（这里指的是几个像素的偏移）十分敏感，但是，我们希望达到的效果是：在右边能识别出照片里的一只猫，在左边（换个环境）也同样能识别出。

另外，在最后一层中，我们希望能够直接识别出图像中有一只猫，而不是一些局部的纹理、毛色等信息。所以，需要对学到的模式进行汇聚。

汇聚层有最大汇聚层（max）和平均 汇聚层，最大汇聚层如下；

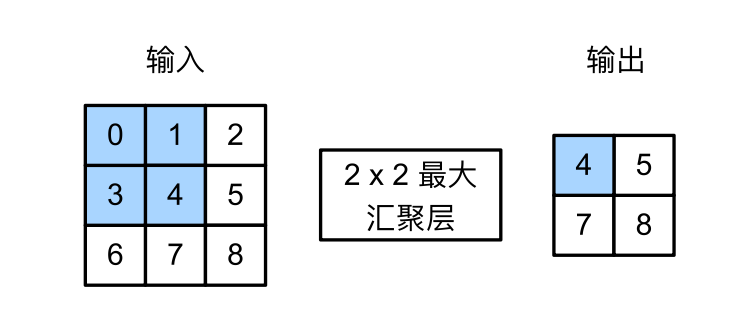
![截屏2023-08-14 12.33.03](./d2l/截屏2023-08-14 12.33.03.png)

这里的汇聚层的大小是$2\times2$的，可以理解成允许物体向右边偏移一个像素；若是换成$3\times3$的话，可以理解成允许左右偏移一个像素。

LeNet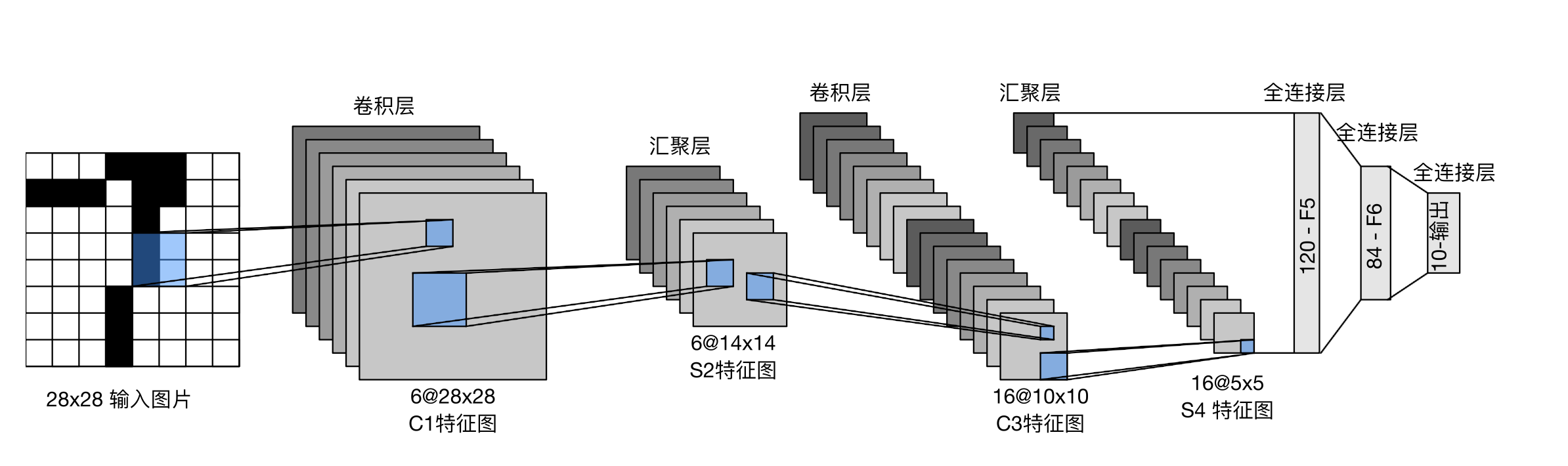

![截屏2023-08-14 14.30.43](./d2l/截屏2023-08-14 14.30.43.png)

上面是完整的架构，下面是网络的定义：

1
2
3
4
5
6
7
8
9
net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

用的是sigmoid激活函数，下面是输出结果：

1
2
loss 0.469, train acc 0.823, test acc 0.813
26794.6 examples/sec on cuda:0

然后将激活函数换成ReLU，结果是：

1
2
loss 0.531, train acc 0.808, test acc 0.767
27731.5 examples/sec on cuda:0

好像差不太多，然后把学习率从1e-2上调到1e-1

1
2
loss 0.318, train acc 0.882, test acc 0.868
27809.8 examples/sec on cuda:0

满意离开。

现代卷积神经网络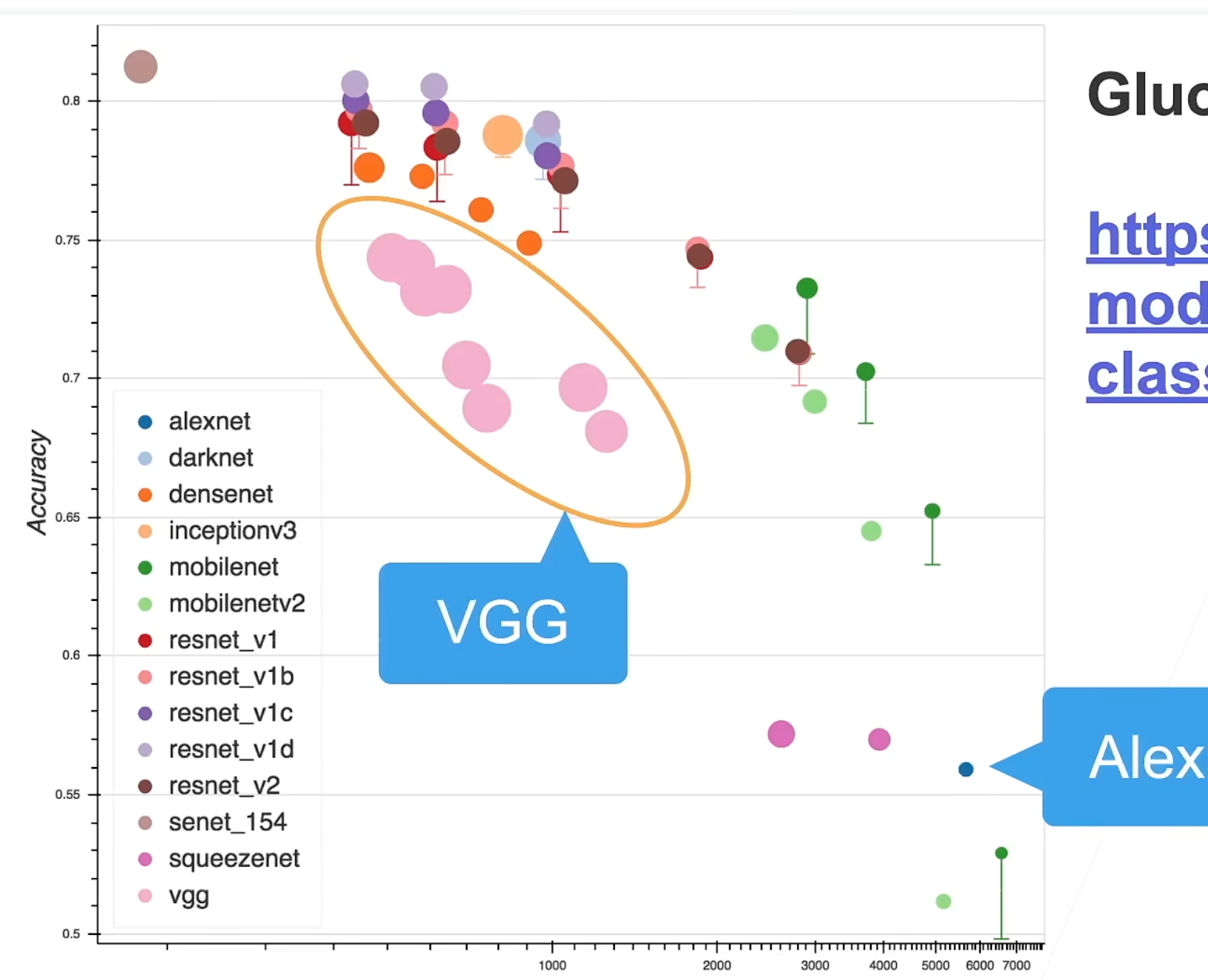

![](./d2l/截屏2023-08-15 13.28.57.png)

上图横坐标是训练难度，纵坐标是精度。

AlexNet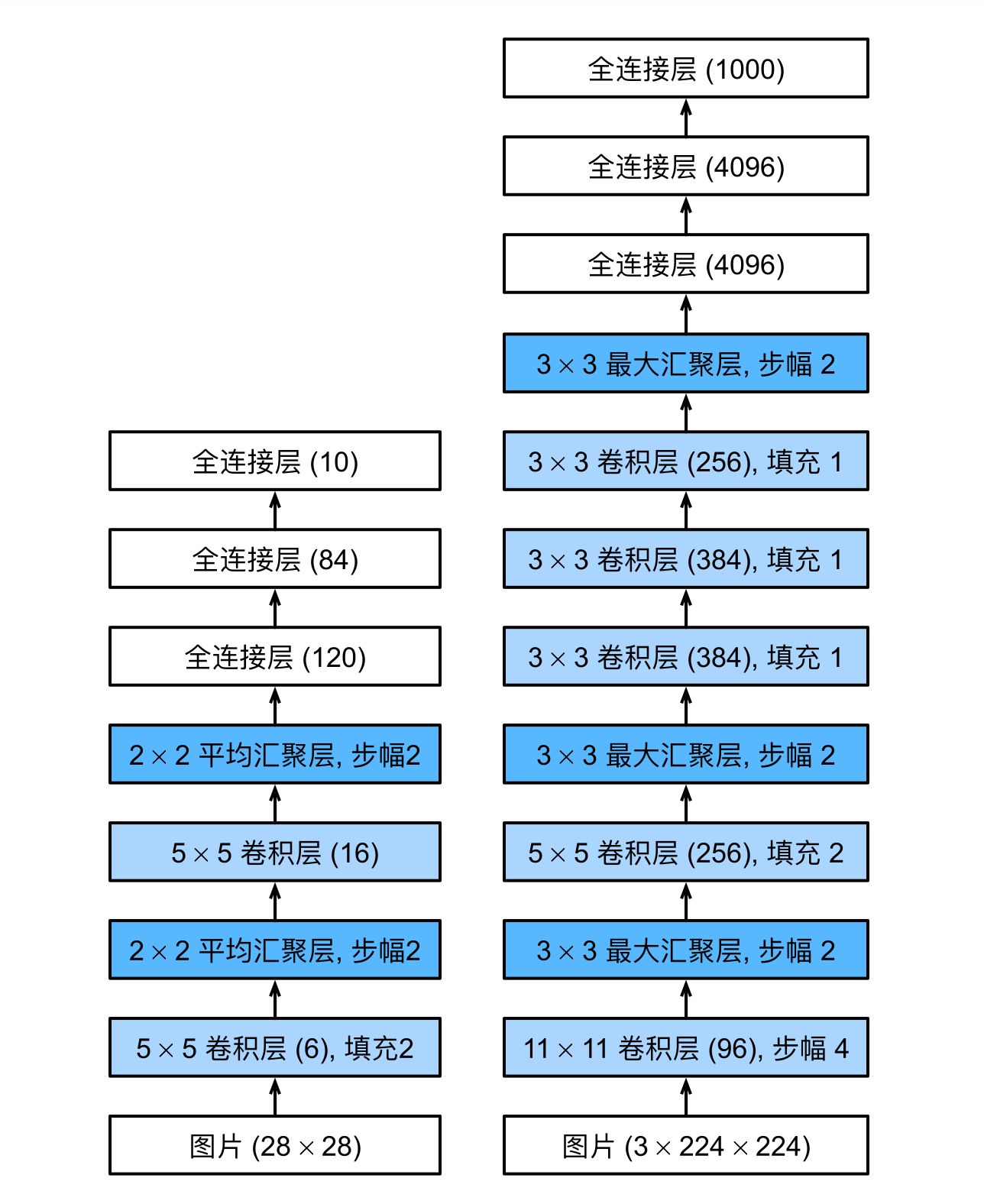

![截屏2023-08-14 20.16.24](./d2l/截屏2023-08-14 20.16.24.png)

上图左为LeNet，右为AlexNet，，可以看到其实AlexNet大致上就是一个更大更肥的LeNet，有几个细节：

  • 激活函数从sigmoid换成了ReLU
  • 输入变成3通道了
  • 采用了Dropout
  • 双GPU

下面是网络的代码形式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
net = nn.Sequential(
    # 这里使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

VGG

AlexNet在当时的提升是非常大的，但是卷积层设计的非常奇怪，没有提供通用的模版，给人一种感觉“我这样设置网络效果就很好”。

于是出现了VGG。

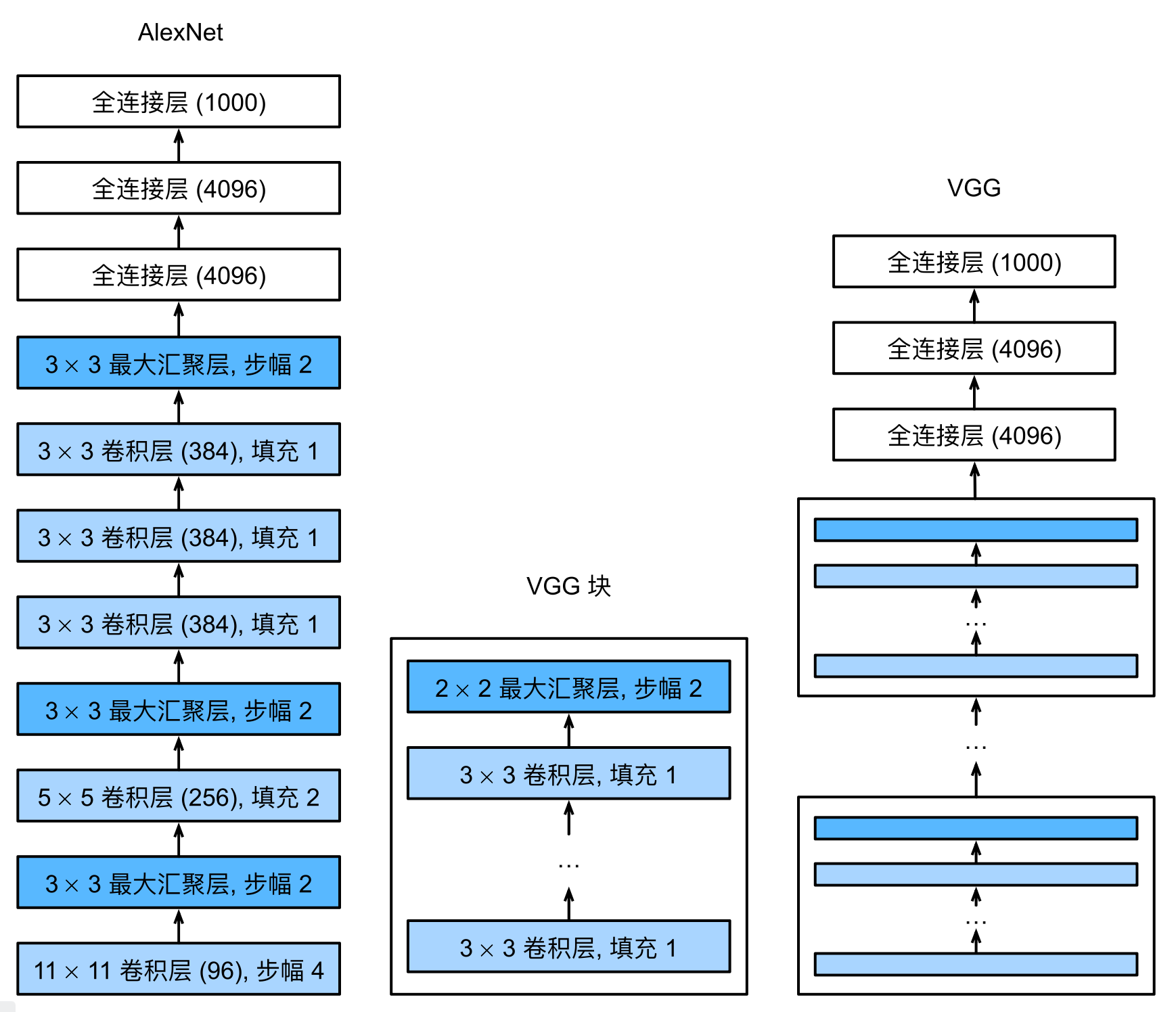
![截屏2023-08-15 12.23.50](./d2l/截屏2023-08-15 12.23.50.png)

与AlexNet不同的是，VGG用的卷积核都是$3\times3$的，而不是$11\times11$的，更小的窗口，带来更深的网络。（从结果上来讲，这样的设计，最后模型的精度确实高很多）。

最原始的VGG：

  • 一个VGG快包含若干个卷积层（$3\times3$的卷积核，padding为1保证输入输出size一样，汇聚层的汇聚窗口为$2\times2$，stride为2，这样使得整个VGG块的输入到输出减半）

然后可以根据设备的计算量，选择使用几个VGG块。

NiN

NiN块的出现在于使用$1\times1$的卷积层来替换最后的全连接层的作用。

全连接层相比于卷积层，有更多的参数个数，这带来的计算量开销和显存开销是非常大的。

![截屏2023-08-15 13.02.06](./d2l/截屏2023-08-15 13.02.06.png)

所以NiN的想法就是去掉全连接层：

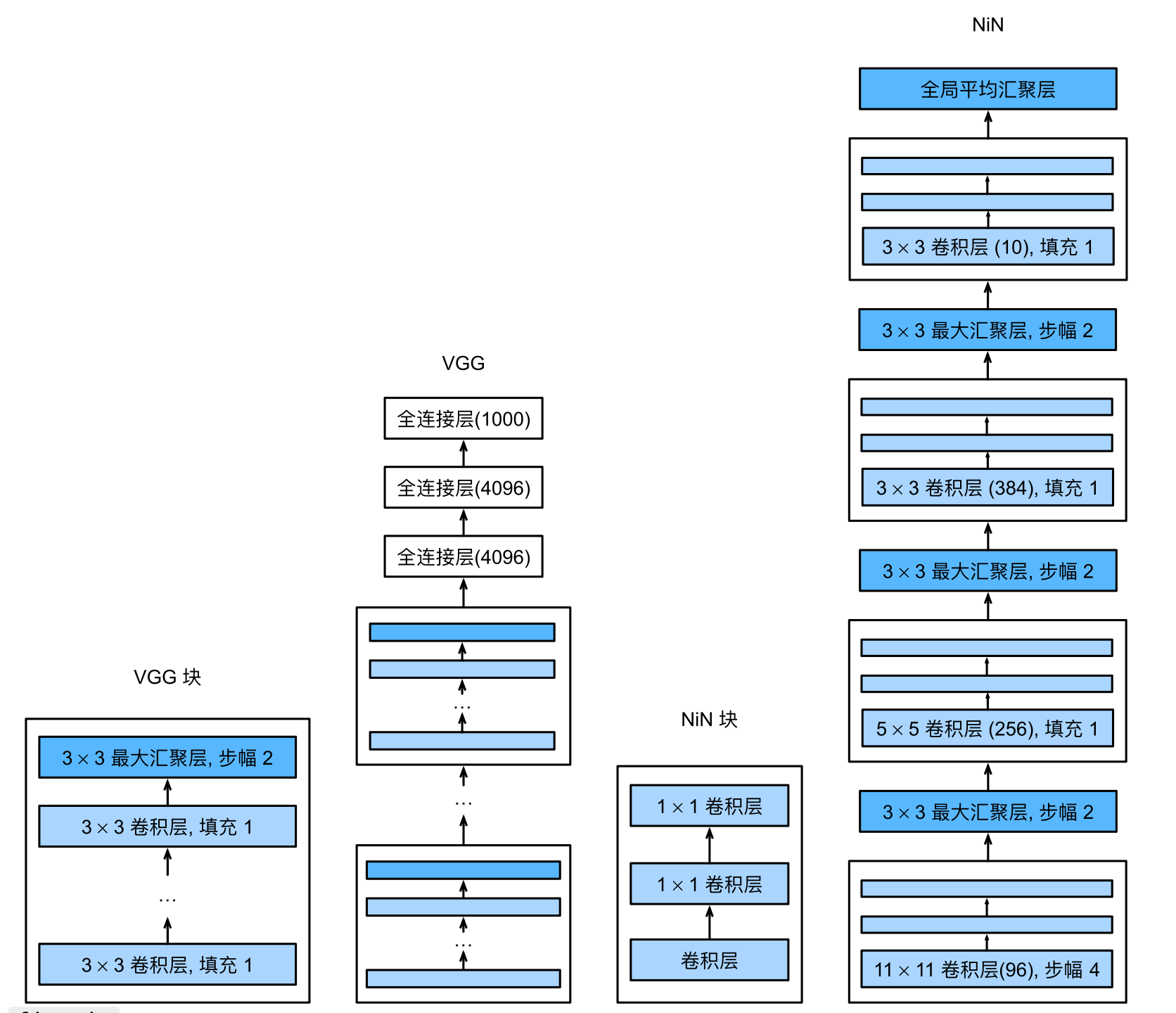
![截屏2023-08-15 13.03.11](./d2l/截屏2023-08-15 13.03.11.png)

GoogLeNet

。。。用“忙里”砸出来的，暂时没什么好看的，其核心就是用下面的Inception块：

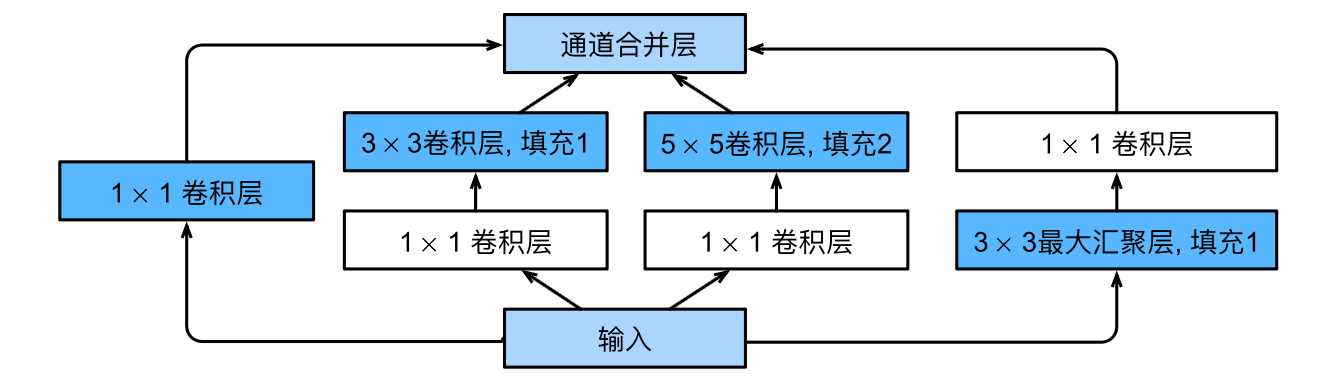
![截屏2023-08-15 17.15.54](./d2l/截屏2023-08-15 17.15.54.png)

整个网络的结构如下：

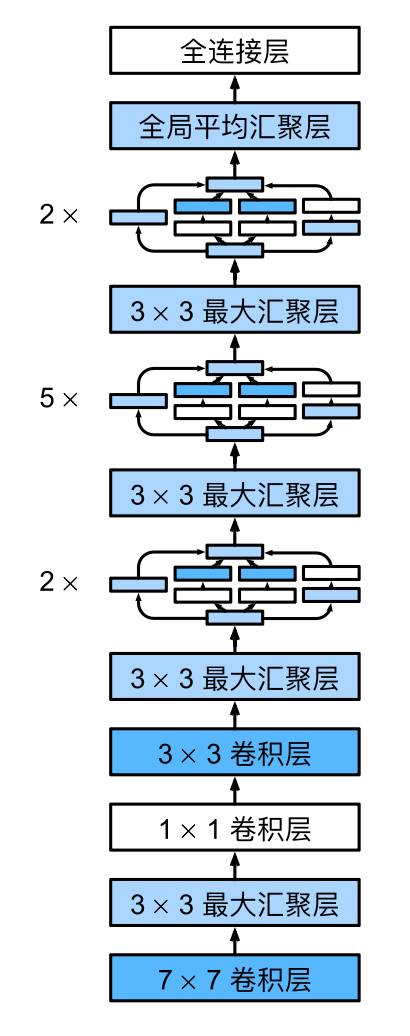
![截屏2023-08-15 17.16.19](./d2l/截屏2023-08-15 17.16.19.png)

后续有些改进也就是改进的Inception块，比如把$5\times5$的卷积核改成$3\times3$，然后把$3\times3$换成2个$1\times7$。总之就是条蚕调出来的，至于能不能用，为什么，没有很多的说法，复现也不是很容易。

batch normalization

批量正则化，他的出现是试图解决这个问题：随着模型的变深，当我们进行backward更新梯度时，靠近输出端的w可以很快的更新，这也就导致上层可以很快的收敛；相反，靠近数据的输入端，由于梯度一直累乘累乘（链式法则求导），所以下面的梯度就更新的很慢，并且，对于不同的batch（这些数据是随机抽取的，可能有很大的不同，在数据分布上），上层的权重能够很快的适应，但是下层，靠近数据输入端的并不能很快适应。越往下，越需要一种方法来解决这个。

批量正则化在干这样一件事，往我们的数据（输入或者输出）中增加噪声，以此来控制我们模型的复杂性。

  • 在MLP中，将batch normalization层放在仿射变换和激活函数之间
  • 在CNN中，将其放在卷积层和激活函数之间

值得注意的是，batch normalization并不一定是正确的，仅仅是现在很多人使用，原因是：精度不一定提升，但是模型的收敛速度很快。

ResNet

整个神经网络其实就是在学习、找到一个合适的函数，或者说学习到一种模式，来解决问题。我们之前了解到的网络可能会出现下图中左边的那种情况：

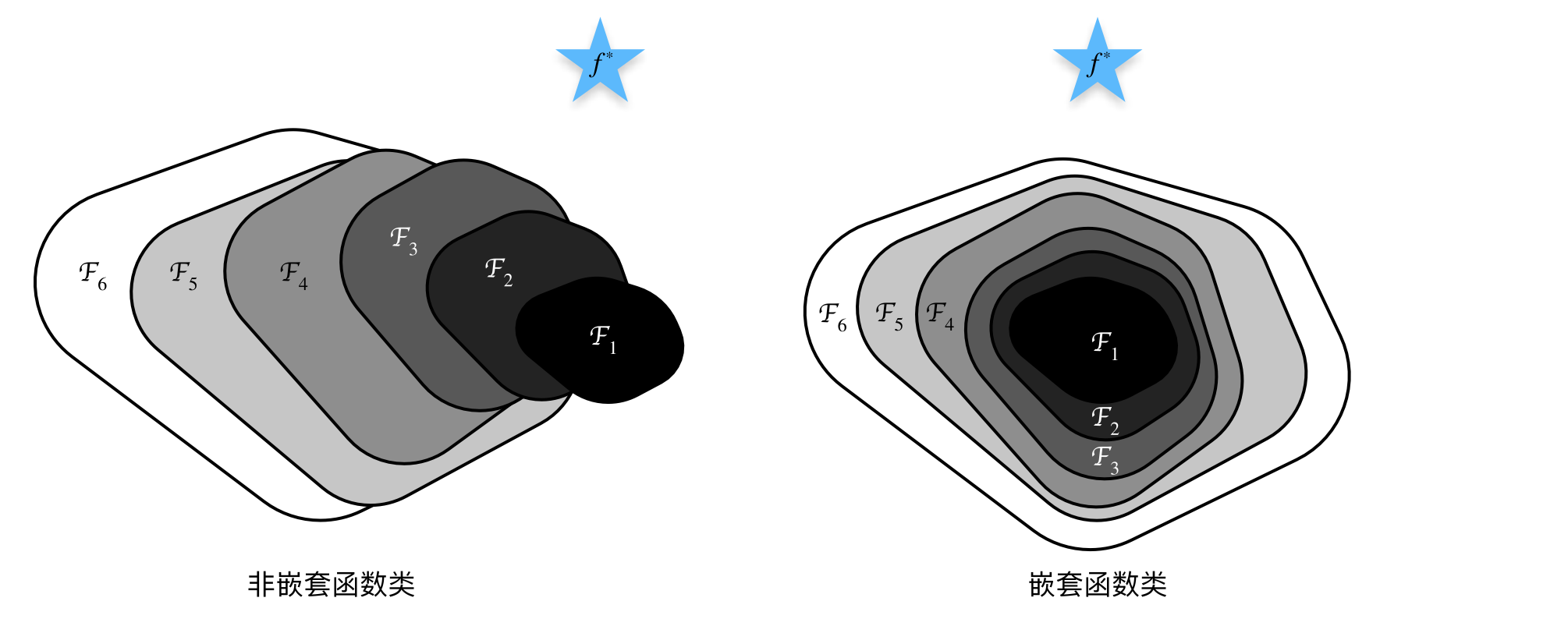
![截屏2023-08-15 19.51.56](./d2l/截屏2023-08-15 19.51.56.png)

训练过程中离最优解越来越远了。但我们理想的效果反而是右图。残差块可以解决这个：

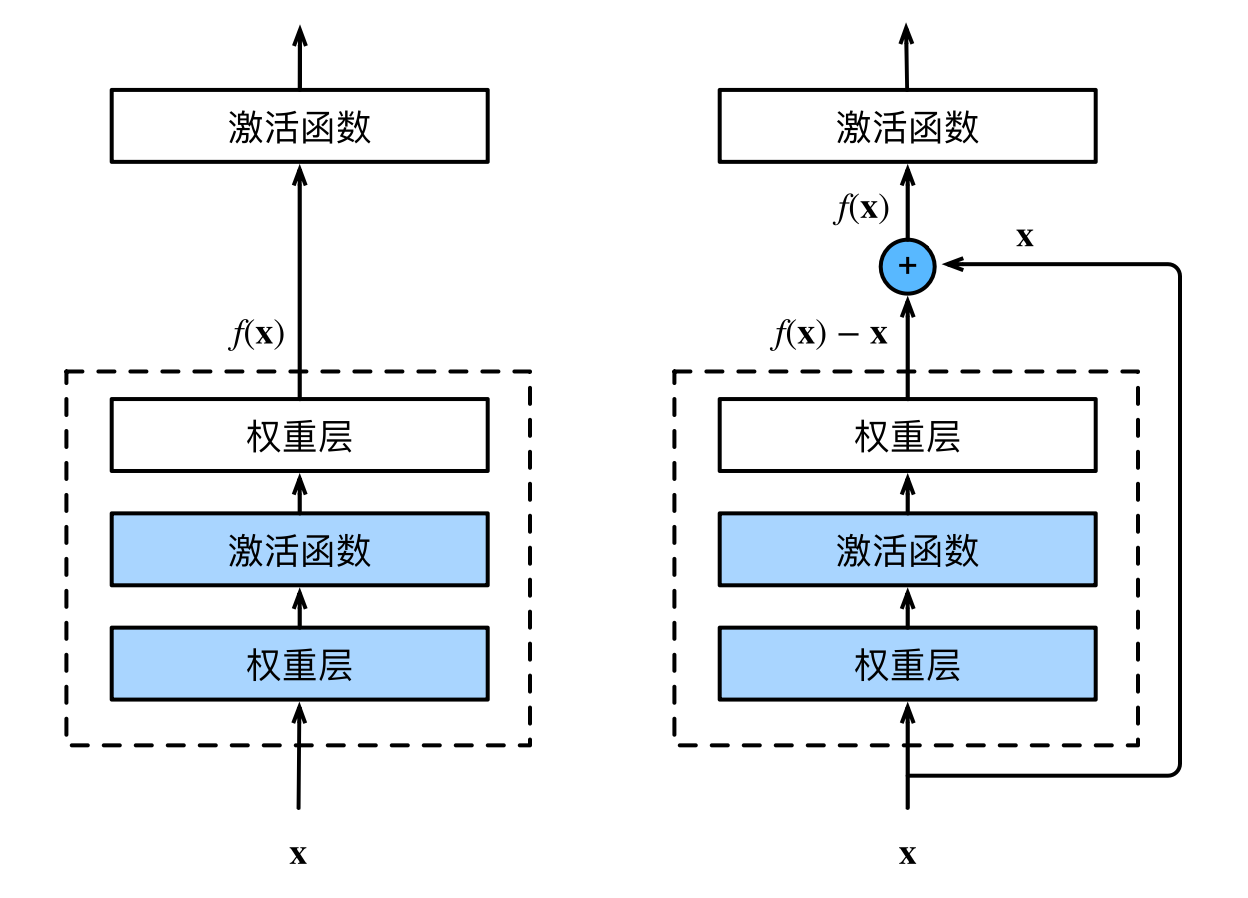
![截屏2023-08-15 19.56.14](./d2l/截屏2023-08-15 19.56.14.png)

可以看到相较于前面的网络，残差块加上了一个前向反馈，这样不管中间有没有学到东西，至少之前学到的x是能够保留的。

另外，残差块就是将乘法转换成了加法，在反向传播求导的过程中，能够加快训练速度。

代码训练–MLP+CNN

这里对前面学到的一些知识用代码复现一下，加深理解，避免遗忘。

线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import random

import torch
import matplotlib.pyplot as plt

true_w = torch.Tensor([2, - 3.4])
true_b = 4.2
X = torch.normal(0, 1, (10000, len(true_w)))
Y = torch.matmul(X, true_w) + true_b  # x是一个矩阵，w是一个列向量，最后乘出来得到一个列向量
Y += torch.normal(0, 0.01, Y.shape)


def data_iter(batch_size, features, labels):
    num = len(features)
    indexes = list(range(num))
    random.shuffle(indexes)
    for i in range(0, num, batch_size):
        batch_indexes = torch.tensor(indexes[i: min((i + batch_size, num))])
        yield features[batch_indexes], labels[batch_indexes]


pred_w = torch.normal(0, 0.01, size=true_w.shape, requires_grad=True)
pred_b = torch.zeros(1, requires_grad=True)
lr = 1e-2
epoch = 5
batch = 30
losses = []
for i in range(epoch):
    for x, y in data_iter(batch_size=batch, features=X, labels=Y):
        l = 0.5 * (torch.matmul(x, pred_w) + pred_b - y) ** 2
        l.sum().backward()
        with torch.no_grad():
            for param in [pred_w, pred_b]:
                param -= lr * param.grad / batch
                param.grad.zero_()
    with torch.no_grad():  # 每一个epoch结束后，测试所有数据的loss
        train_l = 0.5 * (torch.matmul(X, pred_w) + pred_b - Y) ** 2
        print(f'epoch {i + 1}, loss {float(train_l.mean()):f}')
        losses.append(float(train_l.mean()))

plt.plot(range(1, epoch + 1), losses)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.show()

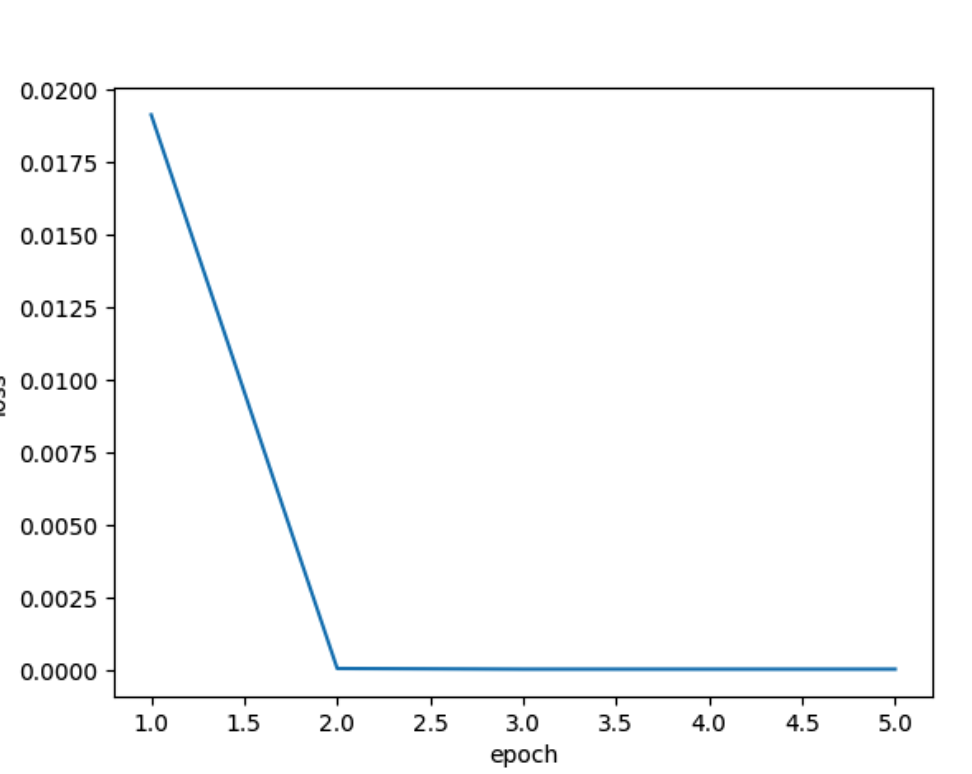
![截屏2023-08-17 13.23.07](./d2l/截屏2023-08-17 13.23.07.png)

softmax线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
import torch
import torchvision.datasets
from torch.utils import data
from torchvision import transforms
import d2l.torch as d2l
import torch.nn as nn
import matplotlib.pyplot as plt

batch_size = 256
num_workers = 0
trans = transforms.ToTensor()  # 以tensor的形式存下来
dev = torch.device("mps")
minist_train = torchvision.datasets.FashionMNIST(
    root="./data",
    train=True,
    transform=trans,  # 将下下来的图片以tensor的形式读进内存
    download=True
)
minist_test = torchvision.datasets.FashionMNIST(
    root="./data",
    train=False,
    transform=trans,
    download=True,
)
train_iter = data.DataLoader(minist_train, batch_size, num_workers=num_workers, shuffle=True)
test_iter = data.DataLoader(minist_test, batch_size)

num_inputs = 1 * 28 * 28
num_outputs = 10
w = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True, device=dev)
b = torch.zeros(size=(num_outputs,), requires_grad=True, device=dev)


def softmax(X):
    X_exp = torch.exp(X)
    fen_mu = X_exp.sum(dim=1, keepdim=True)
    return X_exp / fen_mu


def net(X):
    return softmax(torch.matmul(X.reshape(-1, w.shape[0]), w) + b)


def cross_entropy(y_hat, y):
    return -torch.log(y_hat[range(len(y_hat)), y])


def accuracy(y_hat, y):
    if len(y_hat.shape) > 0 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)  # 取每行的最大值作为预测概率
    cmp = y_hat.type(y.dtype) == y  # 将y_hat转成y同样的数据类型，然后比较得到bool类型，分类问题都可以这样做
    return float(cmp.type(y.dtype).sum())


def evaluate_accuracy(net, data_iter):
    if isinstance(net, nn.Module):
        """
        如果模型是继承自torch.nn.Module的话，那么会自动求梯度，设置成评估模式的意思就是不要求梯度了
        """
        net.eval()
    """设置累加器，需要累加的有：正确预测数，预测总数"""
    metric = d2l.Accumulator(2)
    for x, y in data_iter:
        x, y = x.to(dev), y.to(dev)
        metric.add(accuracy(net(x), y), y.numel())
    return metric[0] / metric[1]


def train_epoch(net, data_iter, loss, updater, lr, params):
    if isinstance(net, nn.Module):
        net.train()  # 累计梯度
    metric = d2l.Accumulator(3)
    for x, y in data_iter:
        x, y = x.to(dev), y.to(dev)
        y_hat = net(x)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            """
            如果采用的是torch的Optimizer，那么下面这样处理
            1. 梯度清零
            2. 反向传播
            3. 自动更新参数
            """
            updater.zero_grad()
            l.backward()
            updater.step()
            metric.add(
                float(l) * len(y),
                accuracy(y_hat, y),
                y.size().numel(),
            )
        else:
            """如果自己手写，那么l出来就是一个向量"""
            l.sum().backward()
            updater(lr, x.shape[0], *params)
            metric.add(
                float(l.sum()),
                accuracy(y_hat, y),
                y.numel()
            )
        """
        :returns loss/n, acc/ n
        """
        return metric[0] / metric[2], metric[1] / metric[2]


def train(net, train_iter, test_iter, loss, num_epoch, updater, lr, params):
    train_acc_list, train_loss_list, test_acc_list = [], [], []
    for i in range(num_epoch):
        train_metrics = train_epoch(
            net=net,
            data_iter=train_iter,
            loss=loss, updater=updater,
            lr=lr,
            params=params
        )
        test_acc = evaluate_accuracy(net, test_iter)
        train_acc_list.append(train_metrics[1])
        train_loss_list.append(train_metrics[0])
        test_acc_list.append(test_acc)
        print(f"epoch: {i + 1}, rain loss: {train_metrics[0]:.2f}, train acc: {train_metrics[1]:.2f}, test acc: {test_acc:.2f}")
    return train_acc_list, train_loss_list, test_acc_list


def updater(lr, batch, *params):
    """在我们手动实现的优化器里面，已经将梯度每次清零了"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch
            param.grad.zero_()


epoch = 100
lr = 1e-1
train_acc_list, train_loss_list, test_acc_list = train(
    net=net,
    lr=lr,
    num_epoch=epoch,
    params=(w, b),
    train_iter=train_iter,
    test_iter=test_iter,
    loss=cross_entropy,
    updater=updater
)
plt.plot(range(epoch), train_acc_list, label="train acc", color="red")
plt.plot(range(epoch), train_loss_list, label="train loss", color="green")
plt.plot(range(epoch), test_acc_list, label="test acc", color="blue")
plt.xlabel("epoch")
plt.ylabel("train/evaluate")
plt.ylim(0, 3)
plt.legend()
plt.show()

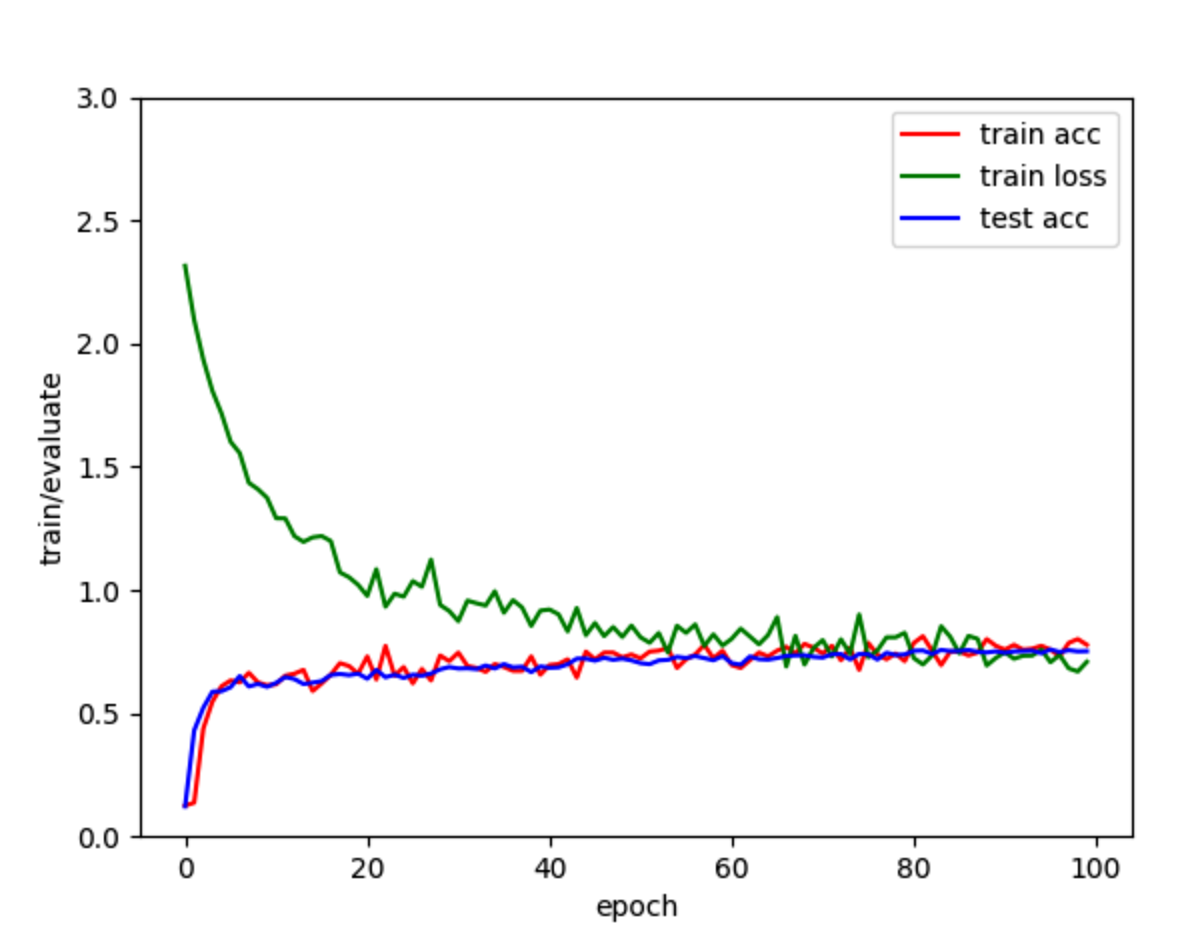
![截屏2023-08-18 09.15.49](./d2l/截屏2023-08-18 09.15.49.png)

MLP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
import torch.utils.data
import torchvision.datasets
import torch.nn as nn
import d2l.torch as d2l
from matplotlib import pyplot as plt

batch_size = 256
minist_train = torchvision.datasets.FashionMNIST(
    download=False,
    transform=torchvision.transforms.ToTensor(),
    train=True,
    root="./data"
)
minist_test = torchvision.datasets.FashionMNIST(
    download=False,
    transform=torchvision.transforms.ToTensor(),
    train=False,
    root="./data"
)
dev = torch.device("mps")
train_iter = torch.utils.data.DataLoader(minist_train, batch_size, shuffle=True)
test_iter = torch.utils.data.DataLoader(minist_test, batch_size)

num_input, num_hiddens, num_output = 1 * 28 * 28, 256, 10
w1 = nn.Parameter(torch.normal(0, 0.01, (num_input, num_hiddens), device=dev, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True, device=dev))
w2 = nn.Parameter(torch.normal(0, 0.01, (num_hiddens, num_output), device=dev, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_output, requires_grad=True, device=dev))


def ReLU(x):
    return torch.max(x, torch.zeros(x.shape, device=dev))


def net(x):
    x = x.reshape(-1, num_input)
    h = ReLU(x @ w1 + b1)
    o = h @ w2 + b2
    return o


loss = nn.CrossEntropyLoss(reduction="none")
num_epoch, lr = 20, 1e-2
updater = torch.optim.SGD(params=(w1, b1, w2, b2), lr=lr)


def acc(y_hat, y):
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    tmp = y_hat.type(y.dtype) == y
    return float(tmp.type(y.dtype).sum())


def train_epoch(net, data_iter, loss, updater):
    if isinstance(net, torch.nn.Module):
        net.train()
    accumulator = d2l.Accumulator(3)
    for x, y in data_iter:
        x, y = x.to(dev), y.to(dev)
        y_hat = net(x)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            updater.zero_grad()
            l.mean().backward()
            updater.step()
            accumulator.add(
                float(l.sum()),
                acc(y_hat, y),
                y.size().numel()
            )
        else:
            print("hahaha")
    return accumulator[0] / accumulator[2], accumulator[1] / accumulator[2]


train_loss_list, train_acc_list, test_acc_list, test_loss_list = [], [], [], []


def train(net, train_iter, test_iter, loss, num_epoch, updater):
    for i in range(num_epoch):
        train_loss, train_acc = train_epoch(net, train_iter, loss, updater)
        if isinstance(net, nn.Module):
            net.eval()
        ctr = d2l.Accumulator(3)
        for x, y in test_iter:
            x, y = x.to(dev), y.to(dev)
            y_hat = net(x)
            ctr.add(
                float(loss(y_hat, y).sum()),
                acc(y_hat, y),
                y.numel()
            )

        test_acc = ctr[1] / ctr[2]
        test_loss = ctr[0] / ctr[2]
        train_loss_list.append(train_loss)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        test_loss_list.append(test_loss)
        print(
            f"epoch: {i + 1}, test acc: {test_acc:.2f}, test loss: {test_loss:.2f}")


train(net, train_iter, test_iter, loss, num_epoch, updater)
# plt.plot(range(num_epoch), train_acc_list, label="train acc", color="red")
plt.plot(range(num_epoch), train_loss_list, label="train loss", color="green")
# plt.plot(range(num_epoch), test_acc_list, label="test acc", color="blue")
plt.plot(range(num_epoch), test_loss_list, label="test loss", color="pink")
plt.xlabel("epoch")
plt.ylabel("train/evaluate")
plt.ylim(0, 3)
plt.legend()
plt.show()

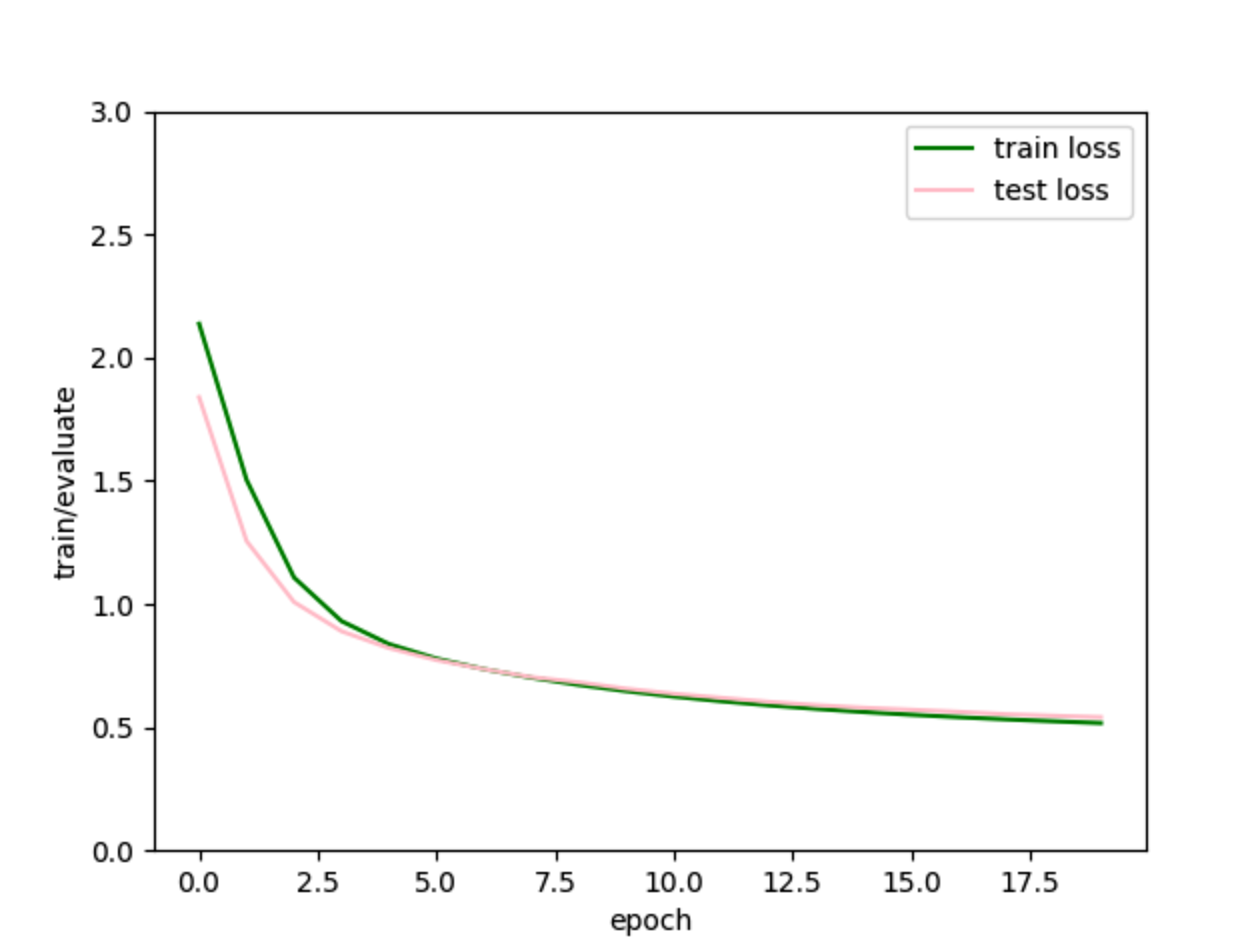
![截屏2023-08-18 10.46.47](./d2l/截屏2023-08-18 10.46.47.png)

跑了20轮，看曲线的走势，test loss快要上升了，可能快过拟合了。

然后试试m1pro的mps和cuda哪个快点：

1
2
3
4
5
6
timer = d2l.Timer()
train(net, train_iter, test_iter, loss, num_epoch, updater)
print(f"time: {timer.stop():.2f} sec")

m1pro: time: 47.91 sec
mx150: 模型太大了，直接爆显存。。。

跑了100轮，看会不会overfitting：

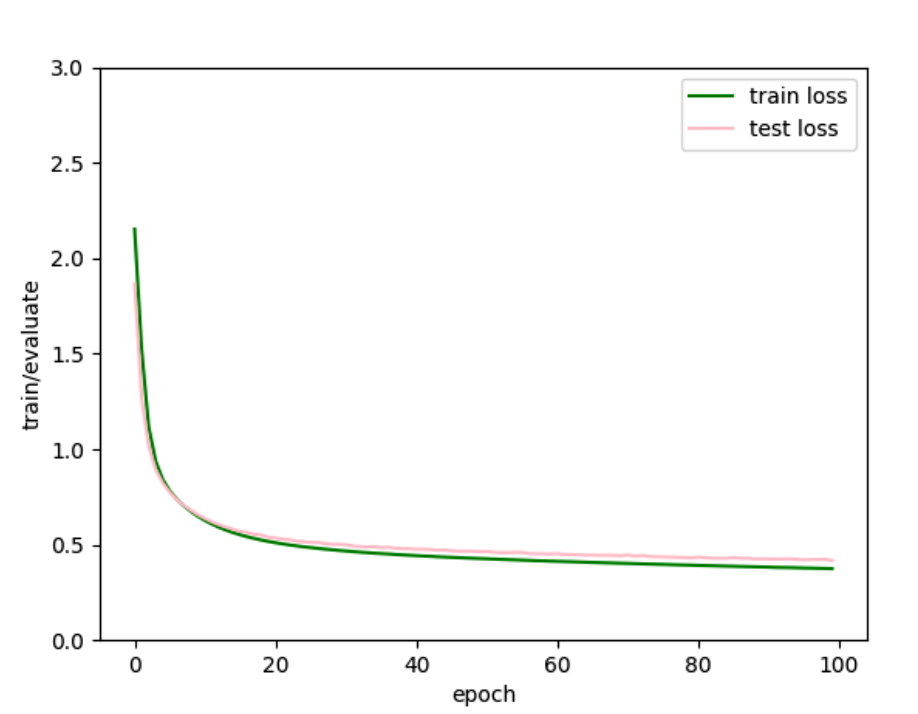
![截屏2023-08-18 11.18.28](./d2l/截屏2023-08-18 11.18.28.png)

貌似也并没有，只是越到后面，梯度越小了，近乎消失了。看样子训练20轮是比较好的了就，从20到100，test acc上升了3个点。

LeNet

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
import torch
import torch.nn as nn
import d2l.torch as d2l
import torchvision.datasets
import torch.utils.data as data
from matplotlib import pyplot as plt

device = torch.device("mps")
batch = 512
minist_train = torchvision.datasets.FashionMNIST(root="./data", train=True, transform=torchvision.transforms.ToTensor(),
                                                 download=False)
minist_test = torchvision.datasets.FashionMNIST(root="./data", train=False, transform=torchvision.transforms.ToTensor(),
                                                download=False)
train_iter = data.DataLoader(minist_train, batch_size=batch, shuffle=True)
test_iter = data.DataLoader(minist_test, batch_size=batch)
net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.ReLU(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.ReLU(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.ReLU(),
    nn.Linear(120, 84), nn.ReLU(),
    nn.Linear(84, 10)
)


def acc(y_hat, y):
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    tmp = y_hat.type(y.dtype) == y
    return float(tmp.type(y.dtype).sum())


train_loss_list, test_loss_list = [], []



def train(net, train_iter, test_iter, epoch, lr, device):
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)

    net.apply(init_weights)
    net.to(device)
    updater = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    accumulator_train = d2l.Accumulator(3)
    for i in range(epoch):
        net.train()
        for x, y in train_iter:
            updater.zero_grad()
            x, y = x.to(device), y.to(device)
            y_hat = net(x)
            l = loss(y_hat, y)
            l.backward()
            updater.step()
            with torch.no_grad():
                accumulator_train.add(
                    l * x.shape[0],
                    acc(y_hat, y),
                    x.shape[0]
                )
        train_acc = accumulator_train[1] / accumulator_train[2]
        train_loss = accumulator_train[0] / accumulator_train[2]
        net.eval()
        accumulator_test = d2l.Accumulator(3)
        for x, y in test_iter:
            x, y = x.to(device), y.to(device)
            y_hat = net(x)
            l = loss(y_hat, y)
            accumulator_test.add(
                l * x.shape[0],
                acc(y_hat, y),
                x.shape[0]
            )
        test_acc = accumulator_test[1] / accumulator_test[2]
        test_loss = accumulator_test[0] / accumulator_test[2]
        test_loss_list.append(test_loss)
        train_loss_list.append(train_loss)
        print(f"epoch: {i + 1}, test_acc: {test_acc:.2f}, test_loss: {test_loss:.2f}")


lr, epoch = 1e-2, 20

if __name__ == '__main__':
    train(net, train_iter, test_iter, epoch, lr, device)
    # plt.plot(range(num_epoch), train_acc_list, label="train acc", color="red")
    plt.plot(range(epoch), train_loss_list, label="train loss", color="green")
    # plt.plot(range(num_epoch), test_acc_list, label="test acc", color="blue")
    plt.plot(range(epoch), test_loss_list, label="test loss", color="pink")
    plt.xlabel("epoch")
    plt.ylabel("train/evaluate")
    plt.ylim(0, 3)
    plt.legend()
    plt.show()

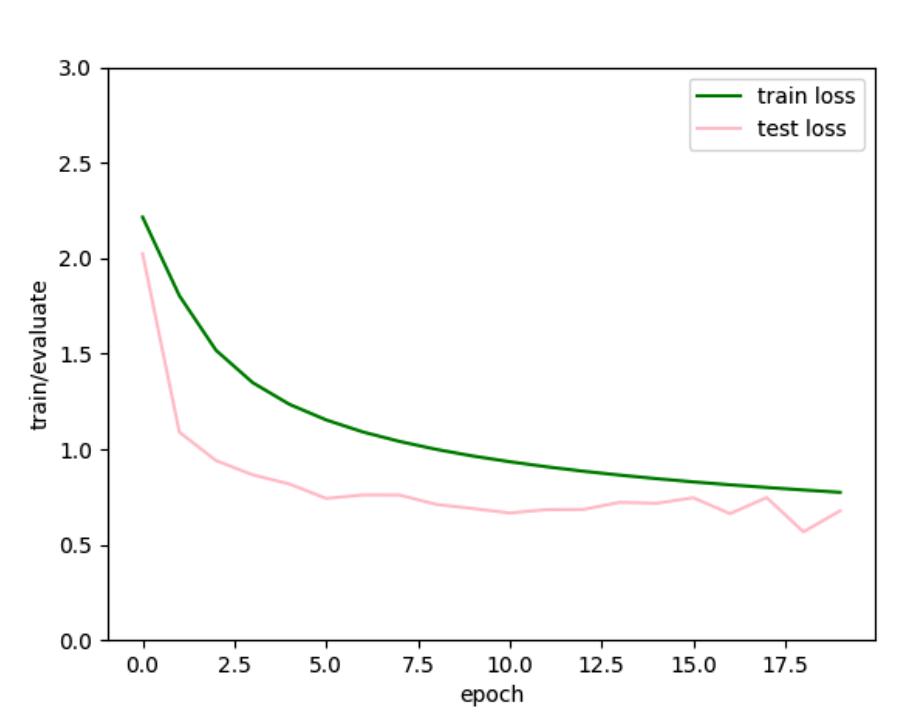
![截屏2023-08-18 13.14.40](./d2l/截屏2023-08-18 13.14.40.png)

貌似有点过拟合了，试着加上L2权重衰减：

1
2
3
4
updater = torch.optim.SGD(net.parameters(), lr=lr, weight_decay=wd)
...
for p in net.parameters():
    l += wd * 0.5 * p.pow(2.0).sum()

![截屏2023-08-18 13.27.50](./d2l/截屏2023-08-18 13.27.50.png)

还是很抖动，降低学习率、增大batch试试。

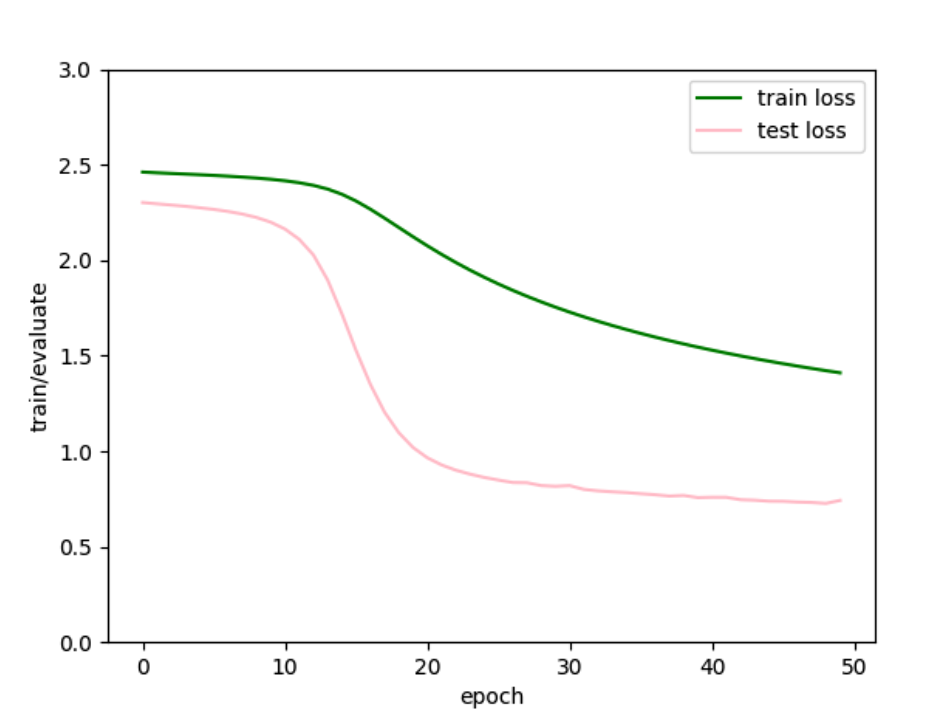
![截屏2023-08-18 13.32.46](./d2l/截屏2023-08-18 13.32.46.png)

曲线确实平滑了点。

然后lr调到4e-3

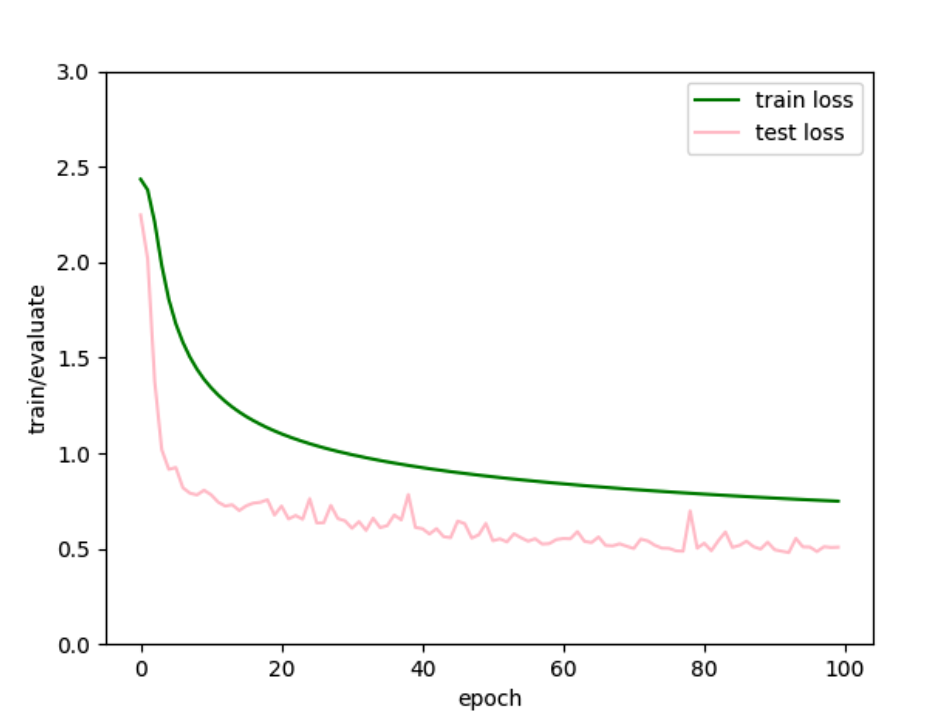
![截屏2023-08-18 13.39.03](./d2l/截屏2023-08-18 13.39.03.png)

学习率1e-3

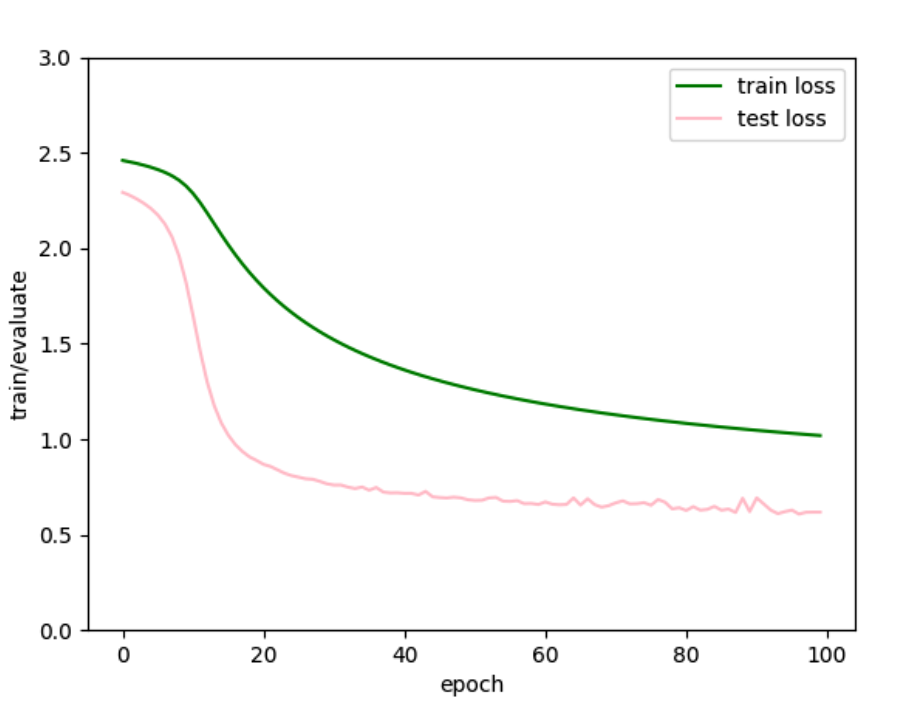
![截屏2023-08-18 13.45.47](./d2l/截屏2023-08-18 13.45.47.png)

AlexNet

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
import torch
import torch.nn as nn
import d2l.torch as d2l
import torch.utils.data as data
import torchvision.datasets
from matplotlib import pyplot as plt
from torchvision.transforms import transforms

batch = 256
trans = [transforms.ToTensor()]
trans.insert(0, transforms.Resize(224))
trans = transforms.Compose(trans)
train_iter = data.DataLoader(
    torchvision.datasets.FashionMNIST("./data", True, transform=trans),
    batch, True)
test_iter = data.DataLoader(
    torchvision.datasets.FashionMNIST("./data", False, transform=trans),
    batch, False)

net = nn.Sequential(
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 10)
)

lr = 1e-2
epoch = 10
device = torch.device("mps")


def train(net, train_iter, test_iter, epoch, lr, device):
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)

    loss = nn.CrossEntropyLoss()
    updater = torch.optim.SGD(params=net.parameters(), lr=lr)
    accumulator_train = d2l.Accumulator(3)
    net.apply(init_weights)
    net = net.to(device)
    train_acc_l, train_loss_l, test_acc_l, test_loss_l = [], [], [], []
    for i in range(epoch):
        net.train()
        for x, y in train_iter:
            updater.zero_grad()
            x = x.to(device)
            y = y.to(device)
            y_hat = net(x)
            l = loss(y_hat, y)
            l.backward()
            updater.step()
            with torch.no_grad():
                if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
                    y_hat = y_hat.argmax(axis=1)
                tmp = y_hat.type(y.dtype) == y
                tmp = tmp.type(y.dtype).sum()
                accumulator_train.add(
                    tmp,
                    float(l) * x.shape[0],
                    x.shape[0]
                )
        train_acc = accumulator_train[0] / accumulator_train[2]
        train_loss = accumulator_train[1] / accumulator_train[2]
        net.eval()
        accumulator_test = d2l.Accumulator(3)
        for x, y in test_iter:
            x, y = x.to(device), y.to(device)
            y_hat = net(x)
            l = loss(y_hat, y)
            y_hat = y_hat.argmax(axis=1)
            tmp = y_hat.type(y.dtype) == y
            tmp = tmp.type(y.dtype).sum()
            accumulator_test.add(
                float(tmp),
                float(l) * x.shape[0],
                x.shape[0],
            )
        test_acc = accumulator_test[0] / accumulator_test[2]
        test_loss = accumulator_test[1] / accumulator_test[2]
        train_acc_l.append(train_acc)
        train_loss_l.append(train_loss)
        test_acc_l.append(test_acc)
        test_loss_l.append(test_loss)
        print(f"epoch: {i + 1}, test_acc: {test_acc:.2f}, test_loss: {test_loss:.2f}, train_acc:{train_acc:.2f}, "
              f"train_loss: {train_loss:.2f}")
    return train_acc_l, train_loss_l, test_acc_l, test_loss_l


if __name__ == '__main__':
    t = d2l.Timer()
    train_acc_l, train_loss_l, test_acc_l, test_loss_l = train(net, train_iter, test_iter, epoch, lr, device)
    print(f"time: {t.stop():.2f} sec")
    plt.plot(range(epoch), train_acc_l, label="train acc", color="red")
    plt.plot(range(epoch), train_loss_l, label="train loss", color="green")
    plt.plot(range(epoch), test_acc_l, label="test acc", color="blue")
    plt.plot(range(epoch), test_loss_l, label="test loss", color="pink")
    plt.xlabel("epoch")
    plt.ylabel("train/evaluate")
    plt.ylim(0, 3)
    plt.legend()
    plt.show()

跑了有点久，这大概就是本地机器的极限了，AlexNet

ResNet

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
#!/usr/bin/env python
# coding: utf-8

# In[9]:


import torch.nn as nn
import d2l.torch as d2l
import torchvision
import torch.utils.data as data
import torch


# # 读取数据集
# 读取Fashion minist数据集，将分辨率Resize得更大点，

# In[5]:


# resize 图片
trans = [torchvision.transforms.ToTensor()]
trans.insert(0, torchvision.transforms.Resize(128))
trans = torchvision.transforms.Compose(trans)

minist_train = torchvision.datasets.FashionMNIST(root="./data", train=True, download=True, transform=trans)
minist_test = torchvision.datasets.FashionMNIST(root="./data", train=False, download=True, transform=trans)

batch = 256
train_iter = data.DataLoader(dataset=minist_train, batch_size=batch, shuffle=True)
test_iter = data.DataLoader(dataset=minist_test, batch_size=batch, shuffle=False)

for x, y in train_iter:
    print(x.shape, y.shape)
    break


# # 构造Residual模块
# 一个residual模块应该包含下面几个部分：
# - 3*3 conv
# - bn
# - relu
# - 3*3 conv
# - bn
# - 输出部分和x同时作为加法器的输入，x可以通过1*1的conv变换通道
# - relu

# In[14]:


import torch.nn.functional as F


class Residual(nn.Module):
    def __init__(self, input_channels, output_channels, use_1_1conv=False, stride=1):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=input_channels, out_channels=output_channels, kernel_size=3, stride=stride,
                               padding=1)
        self.conv2 = nn.Conv2d(in_channels=output_channels, out_channels=output_channels, kernel_size=3, padding=1)
        if use_1_1conv:  #用1*1的卷积核给X做变换
            self.conv3 = nn.Conv2d(in_channels=input_channels, out_channels=output_channels, kernel_size=1,
                                   stride=stride)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(output_channels)
        self.bn2 = nn.BatchNorm2d(output_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3 is not None:
            X = self.conv3(X)
        return F.relu(Y + X)


t = Residual(3, 3)
X = torch.rand((4, 3, 9, 9))
t(X).shape


# # 构造ResNet块
# 有了residual模块，我们就可以构造自己的resnet block了，可以在其中添加若干个residual

# In[39]:


def resnet_block(in_channel, out_channel, num_residual, is_first=False):
    blk = []
    for i in range(num_residual):
        if i == 0 and is_first == False:
            blk.append(
                Residual(in_channel, out_channel, use_1_1conv=True, stride=2))
        else:
            blk.append(Residual(out_channel, out_channel))
    return blk


# # 构造ResNet

# In[31]:


'''
kernel=3, padding=1
kernel=7, padding=3
...
都不会改变矩阵的形状，经过该网络后，是stride把高宽减半了
'''
b1 = nn.Sequential(
    nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
    nn.BatchNorm2d(64), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
X = torch.rand(4, 1, 16, 16)
b1(X).shape


# In[41]:


b2 = nn.Sequential(*resnet_block(64, 64, 2, is_first=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))


# In[42]:


net = nn.Sequential(
    b1, b2, b3, b4, b5,
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten(),
    nn.Linear(512, 10)
)


# In[46]:


X = torch.rand(size=(1, 1, 128, 128))
i = 0
for layer in net:
    i += 1
    print(f"{i} layer input shape: {X.shape}")
    X = layer(X)
    print(layer.__class__.__name__, 'output shape:\t', X.shape)

net.parameters()


# # 开始训练

# In[71]:


def acc(y_hat, y):
    """返回预测正确的类数"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    res = y_hat.type(y.dtype) == y
    res = res.type(y.dtype).sum()
    return float(res)

    # def init_weight(m):
    #     nn.init.xavier_uniform_(m.weight)


def init_weights(m):
    if type(m) == nn.Linear or type(m) == nn.Conv2d:
        nn.init.xavier_uniform_(m.weight)


class TTList:
    def __init__(self, num):
        self.ttl = []
        for i in range(num):
            self.ttl.append([])

    def push(self, elements):
        i = 0
        for e in elements:
            self.ttl[i].append(e)
            i += 1


def train(train_iter, test_iter, net, lr, epoch, device):
    net = net.to(device)
    net.apply(init_weights)
    loss = nn.CrossEntropyLoss()
    updater = torch.optim.SGD(net.parameters(), lr)
    ttl = TTList(4)
    for i in range(epoch):
        net.train()
        accumulator_train = d2l.Accumulator(3)
        for x, y in train_iter:
            updater.zero_grad()
            x = x.to(device)
            y = y.to(device)
            y_hat = net(x)
            l = loss(y_hat, y)
            l.backward()
            updater.step()
            with torch.no_grad():
                accumulator_train.add(acc(y_hat, y), float(l) * x.shape[0], x.shape[0])
        train_acc = accumulator_train[0] / accumulator_train[2]
        train_loss = accumulator_train[1] / accumulator_train[2]
        net.eval()
        accumulator_test = d2l.Accumulator(3)
        for x, y in test_iter:
            x, y = x.to(device), y.to(device)
            y_hat = net(x)
            accumulator_test.add(acc(y_hat, y), float(loss(y_hat, y)) * x.shape[0], x.shape[0])
        test_acc = accumulator_test[0] / accumulator_test[2]
        test_loss = accumulator_test[1] / accumulator_test[2]
        ttl.push([train_acc, train_loss, test_acc, test_loss])
        print(
            f"epoch {i + 1}\ntrain acc: {train_acc:.2f}, train loss: {train_loss:.2f}\ntest acc: {test_acc:.2f}, test_loss: {test_loss:.2f}")
    return ttl


# In[72]:


lr = 1e-2
epoch = 20
batch = 256
device = torch.device("mps")
train(train_iter, test_iter, net, lr, epoch, device)

跑了一轮就有很好的效果：

1
2
3
epoch 1
train acc: 0.81, train loss: 0.58
test acc: 0.81, test_loss: 0.50

CV首选！

RNN

之前从MLP学到CNN，CNN的特点是很适合处理空间信息，能够捕捉到像素级别的特征。对于CNN的数据集，我们假设数据是服从独立同分布的，但是，现实生活中很多东西并不都是独立的：

  • 电影中的视频帧
  • 一篇作文的每一个字
  • 人的脑信号
  • 在网上发言评论
  • …

CNN并不能处理这样的数据，所以这时设计出了RNN：循环神经网络

序列模型

自回归模型

有两种自回归模型：

  • 自回归模型：假设当前的x只和过去的$\tau$个变量有关，于是我们可以根据过去$\tau$个变量，训练出一个MLP或者NN，这样有个好处是每次我们的输入都是固定个数的，都是$\tau$个
  • 隐变量自回归模型：隐变量模型是在当前引入了一个隐变量，当前的输入和隐变量h以及前一时刻的x有关，可以用下图表示

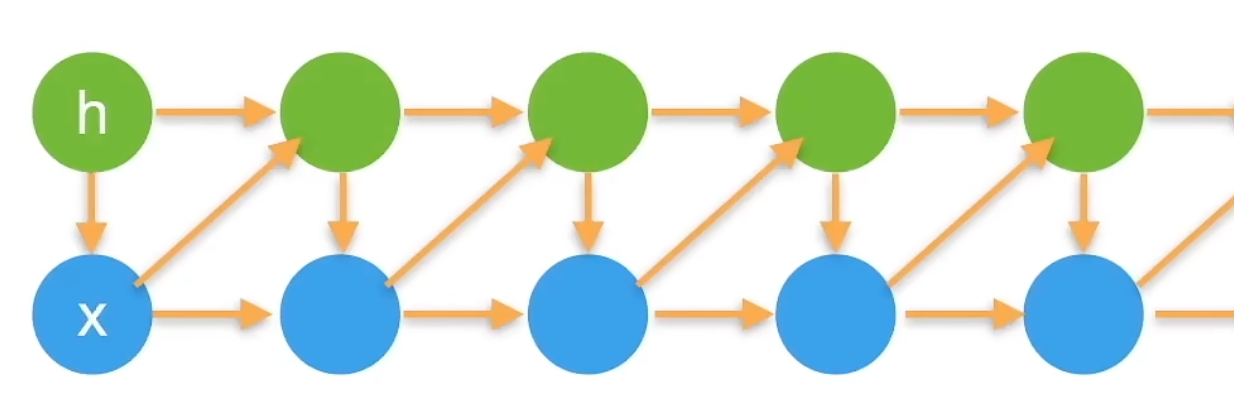
![截屏2023-08-16 13.35.41](./d2l/截屏2023-08-16 13.35.41.png)

马尔可夫模型就是根据前$\tau$个数据进行估计。如果$\tau=1$我们就得到一个一阶的马尔可夫模型。

语言模型